それは、点対称は点を中心に180°回転するためです。 慣れてくれば、首をひねらずに頭の中だけで、180°回転することもできる子供もいますが、図形が苦手な子供はどうしても首をひねってしまいます。 そんな時は、『問題用紙を回していいよ。 』と言う場合が多いです。 目次 書き方さえわかれば、線対称も点対称もこわくない 基本線対称と点対称50 点 対称 書き方 学習支援 まなびの函 中1 平面図形 4 対称な図形 点対称な図形のかき方 Youtube 小学6年算数 点対称な図形の描き方 Youtube 平面図形 点対称な図形のかき方 中学数学形を書き、線対称・点対称の図 形の書き方を知りましょう。書 対称・点対称の図形を書きましょ め 線対称、点対称の図形の書き方を 考えよう。 1 p381の問題をノートに書く。 いた図形はノートに貼りましょ う。今度は自分で図形を考えて線 教科書 授業用
Tossランド 点対称な図形 作図
点対称の書き方小学生
点対称の書き方小学生- 1 「4」を教師が読む。点対称の作図である。線対称よりも難しい。しかし、「やりなさい」と 指示すれば、クラスの3分の2はできる。大切なのは残り3分の1の子の指導だ。 なかでも特に低位の数名は、おそらくまったく手が出ないはずだ。3.点群 どのような対称操作によっても移動しない共通の点を有するものに存在する対称操作の集合 を点群という 点群を表す記号:Shönflies の記号 Cn 群、Dn 群、Cnv 群、Cnh 群、 Dnh 群、Dnd 群、Sn 群、 多面体群(T、Th、Td、O、Oh)など 演習 1



小6算数 対称な図形 点対象 指導アイデア みんなの教育技術
中1 作図 円の中心を求める方法を解説 数スタ 点 対称 書き方 点 対称 書き方⑤はマス目を利用して反転させ真似して書く。 ③④は、線abで紙を折る。 折った紙の裏側から線をなぞり書きして、 表側から再度書く。 ③④は、定規とコンパスを使って書く。 元の絵にある直線部分を定規で延長させて書き、線ab上にコンパスの針を刺して同じ長さを写し取る。書き順 (筆順)・書き方 (文字を正しく美しく書く為の注意点) 美漢字の書き方 美漢字を書けるようになりたい方は、 上記の字を手本に、 自分で漢字を書いてみて下さい。 そして、 自分で書いた字と 手本との違いを比較して、反省する事が大事 です
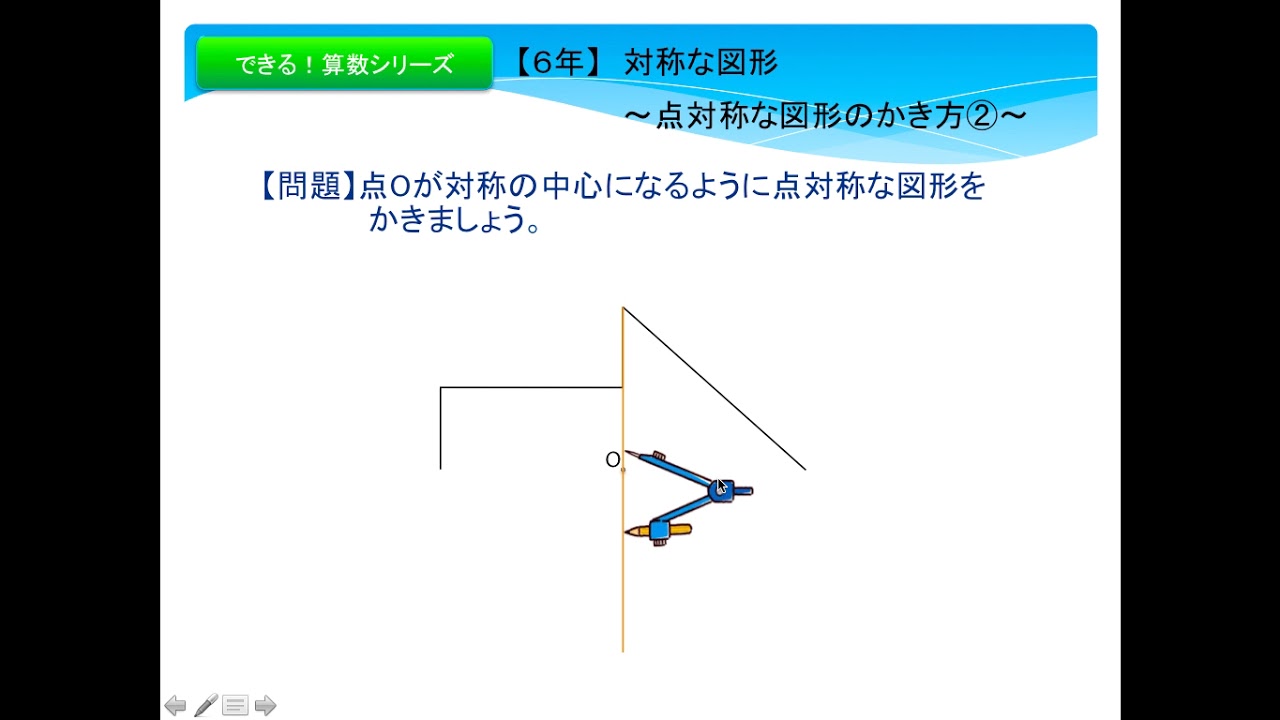
Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV recommendations To avoid 2 「点対称な形のものに『点対称』と書きなさい。」 指名。「いくつありますか。」「3つ書いていない人は探しなさい。」(ヒント)答え合わせ。 3 「また問題」。「線対称な形に『対称の軸』を書き入れなさい。 点対称を作図するのは難しい 下のような図に、点Oを中心に点対称をかくとします。 まずは、ポイントとなるかどに印をつけます。 「かどをえんぴつでぐりぐりしなさ〜い」 次に、そのぐりぐりに端から順番をつけていきます。 つけた順番通りに、点Oを通って点対称なところに印と順番をつけていきます。 ものさしを使ってもいいし、目もりを読み取ら
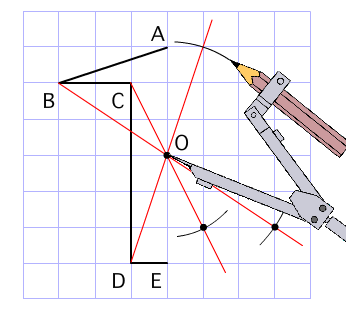
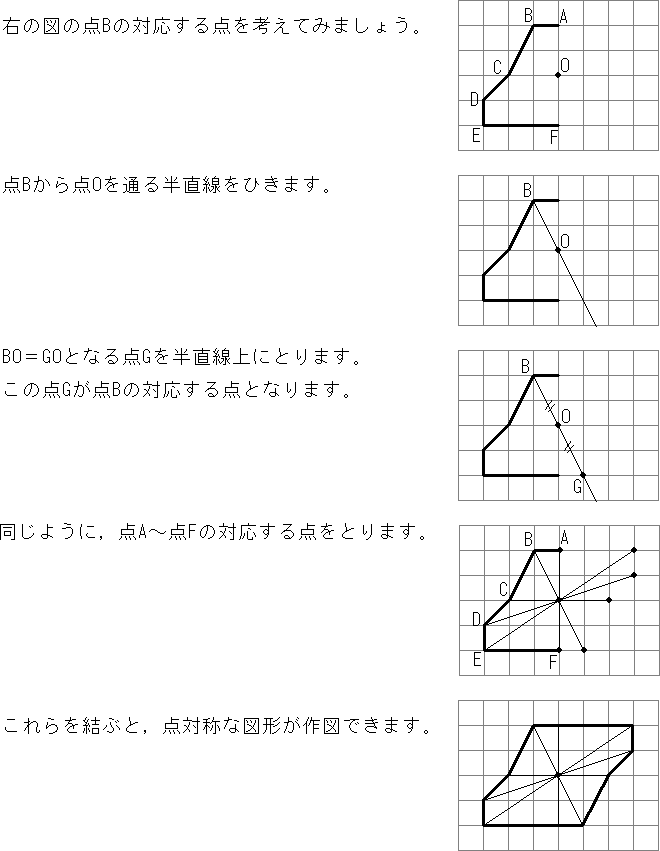
点対称な図形の書き方 点対称な図形の書き方は、対称の中心と対応する点を直線で結ぶことがポイントとなります。 下の図で点oを中心とした点対称な図形を書く場合 各頂点から点oを通る直線を書きます。そして点oから頂点と同じな長さになるところに点をとります。誰か助けて書き方を教えて(´;ω;`) 0 回答 ベストアンサー Studydoctor線対称 点対称な図形の書き方 中学1年数学 Studydoctor 小学6年生の算数 点対称な図形 問題プリント ちびむすドリル
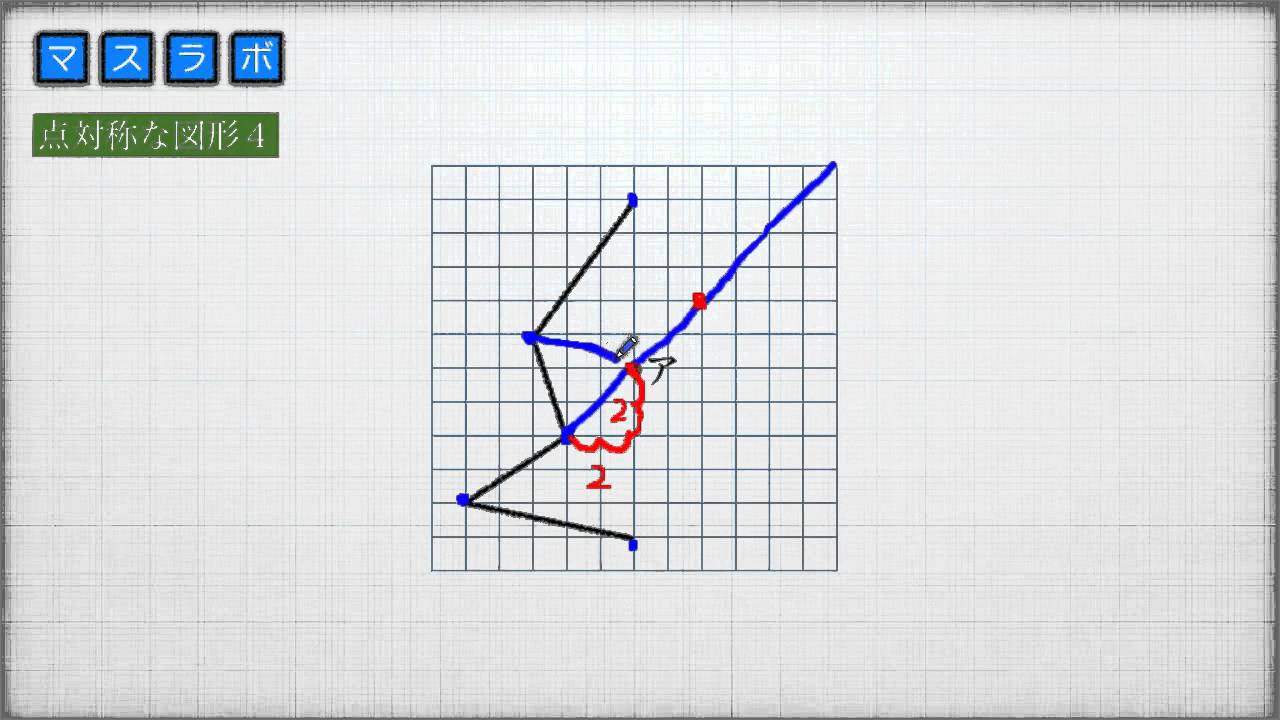



小学校6年 点対称な図形4 点対称な図形をかいてみよう Youtube



点対称な図形
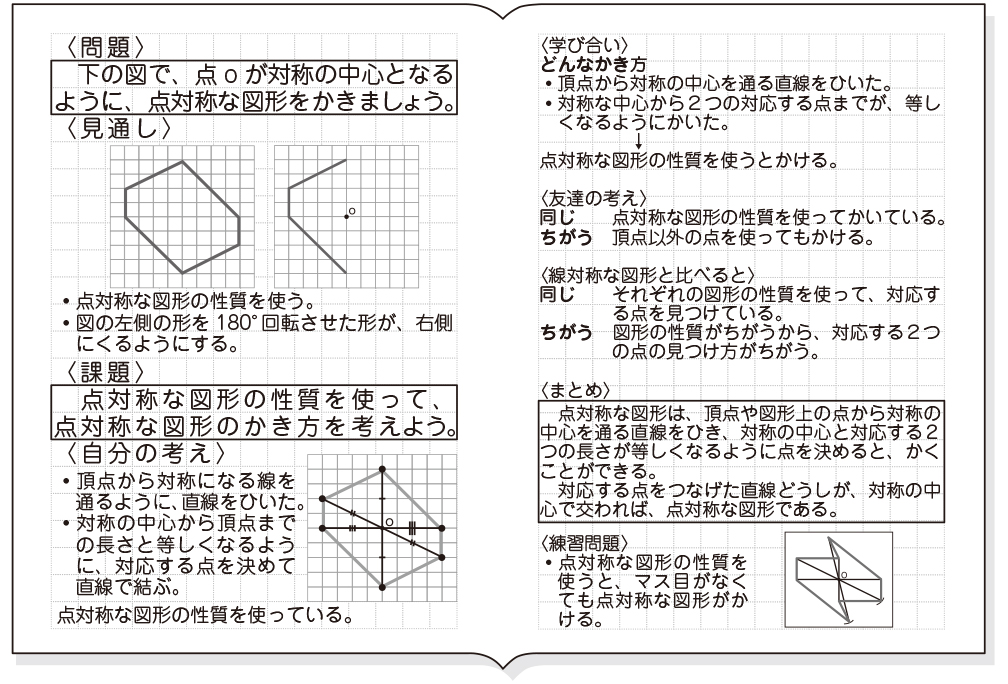
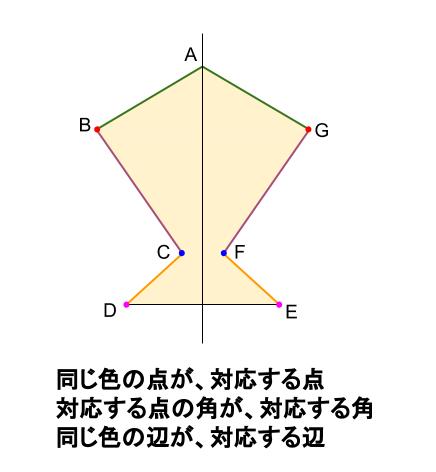
点対称の図形の書き方がわかりません 教えてください ベストアンサー:図形のそれぞれの頂点から定規で点に向かって線を引く この線は伸ばしておく コンパスで針を点におき、頂点には鉛筆をおいてくるっと 伸ばした線とコンパスの交わったことろ線対称・点対称の見分け方 図形の上に縦線を引く(イメージでOK) 図形を180°回転させる 線対称: 180°回転させるまでに左右対称になる瞬間がある(左右対称になった回数が対称の軸の本数) 点対称: 180°回転させた時、元の図形の形と一致する 左右 対応する辺の長さや角の大きさについて調べると、どちらもそれぞれ等しくなっていました 。 (C1) 線対称な図形の時のように、対応する点Aと点D、点Bと点E、点Cと点Fを直線で結んでみました。 すると、全て対称の中心Oで交わっていました。 (C2) C2さんに付け足しで、対称の中心Oから対応する2つの点までの長さが等しくなっていました 。 では、このように



平面図形 5ステップでできる 点対称移動の作図 書き方 Qikeru 学びを楽しくわかりやすく



線対称な図形の書き方と点対称な図形の書き方を教えてくださいお願いします Yahoo 知恵袋
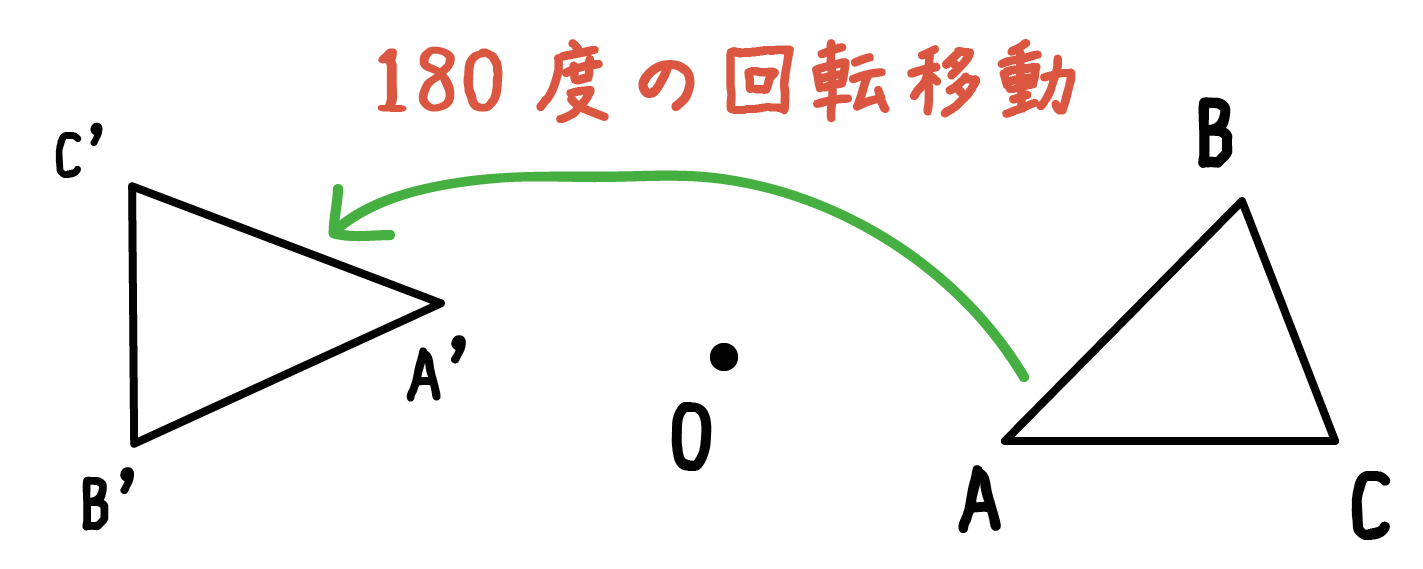
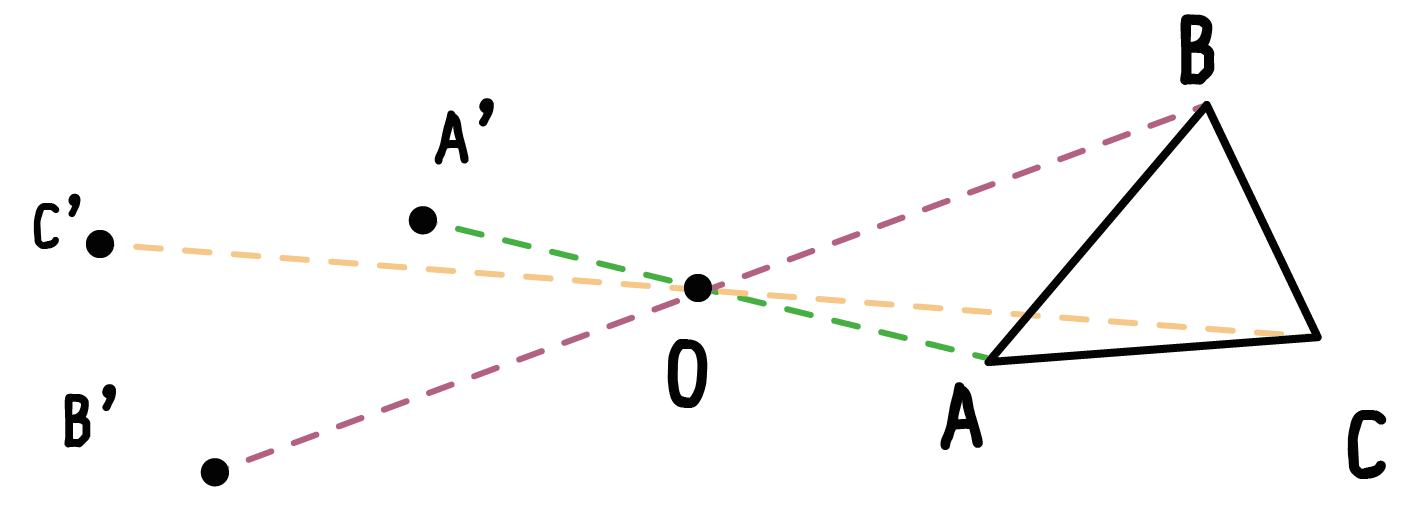
・線対称な図形の意味、性質、作図 ・点対称な図形の意味、性質、作図 ・四角形、三角形、正多角形と対称 小学生・中学生が勉強するならスクールtv。全国の学校の教科書に対応した動画で学習できます。授業の予習・復習にぴったり。まとめ:回転移動の書き方はたった5つのステップで 3点をつないで、眉の輪郭を描いていきます。 下書きをするイメージで、自分が分かる程度に薄く描きましょう。 書き終えたら両方の眉毛を見比べて、左右対称になっているか確認します。 眉の形はこの段階で決まるので、入念にチェックしましょう。 点対称移動は簡単! 各頂点から中心までの移動を調べ、中心から同じだけ移動したところに点を取ります。 まずは頂点aの移動を考えてみましょう。 点aから点oまでは、左1と下4だけ移動すればいいですね。



Studydoctor線対称 点対称な図形の書き方 中学1年数学 Studydoctor
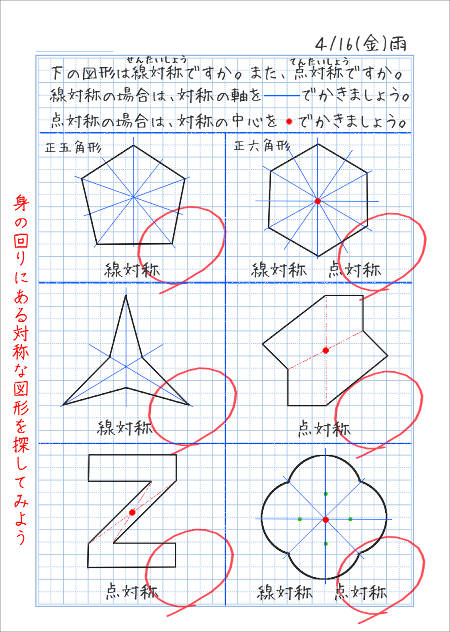



線対称と点対称の自主学習ノート 家庭学習レシピ
線対称・点対称対称な図形①|小6算数①豊橋の学習塾 Duration 447 豊橋の個別指導型学習塾「とよはし練成塾」 17,368 views 対称移動(線対称)の書き方がよくわからない?書き順 (筆順)・書き方 (文字を正しく美しく書く為の注意点) 美漢字の書き方 美漢字を書けるようになりたい方は、 上記の字を手本に、 自分で漢字を書いてみて下さい。 そして、 自分で書いた字と 手本との違いを比較して、反省する事が大事 です点対称な図形のかき方 中心点や対応する点や線に気づかせます。また、定規やコンパスの使い方を聞かれた時は教えます。 点対称図形の書き方 対称の中心が図形の辺にある場合 ↓ 動画作成協力・・動くイラストフリー素材



平面図形 5ステップでできる 点対称移動の作図 書き方 Qikeru 学びを楽しくわかりやすく



3
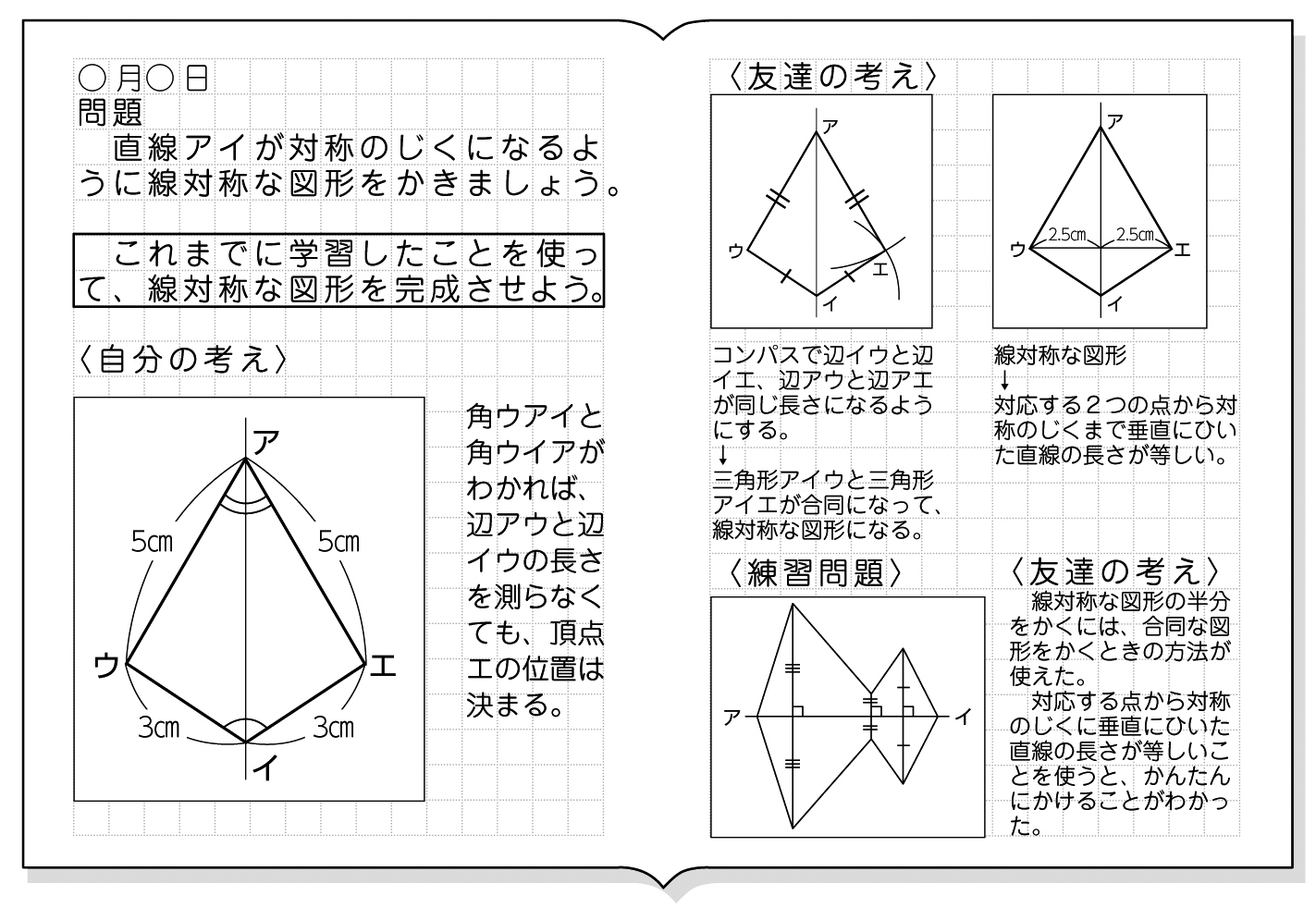
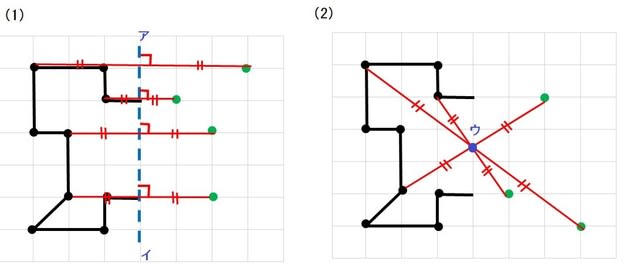
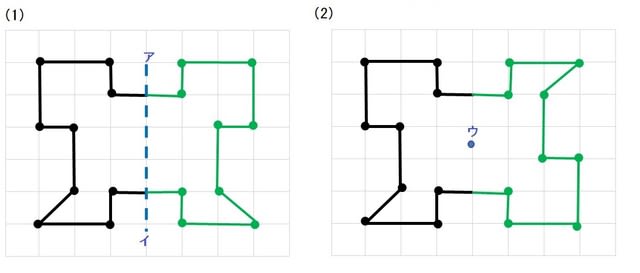
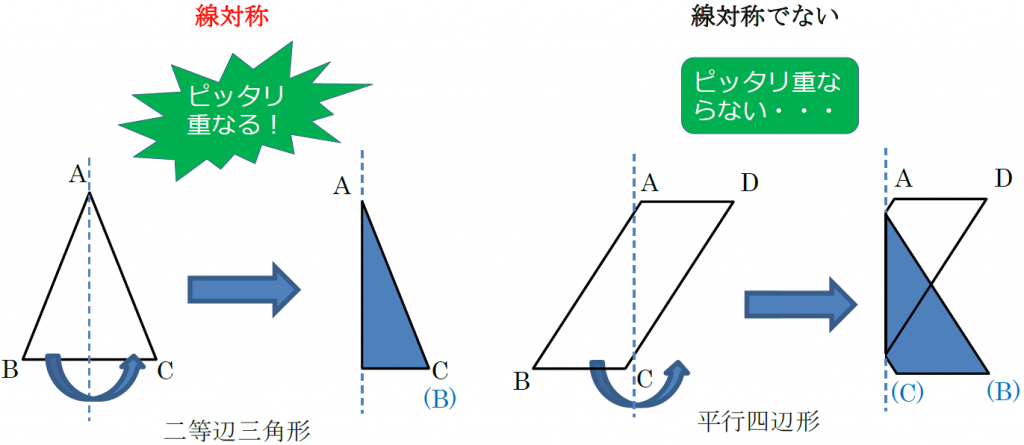
ヒントにしたり、やり方を確認したりしてみてね☆ 対称な図形をかくときは、 対応する頂点を見つけると カンタンにかくことができるよ! ① 頂点から、点O(中心)を通る直線を少し長めに引く 後で、この直線上に点を打つので、算数(対称な図形) 〇線対称のかき方 ① ②それぞれの点を通り, 直線アイに垂直な線を引く。 (簡単に等しい点をとる方法を考えてみよ う!) ③ 点を結ぶ。 〇点対称の書き方。 直線アイまでの長さと等しい点をとる。 点を結ぶ。 ② 対応する点をとる。この図形は、点対称な図形といえるかな? いえる いえない 折り紙を切ったり、はりつけたりして、線対称な図形や点対称な図形 を作ってみましょう。 ※合同な図形を2つ作ると、線対称な 図形や点対称な図形をつくること ができるよ!
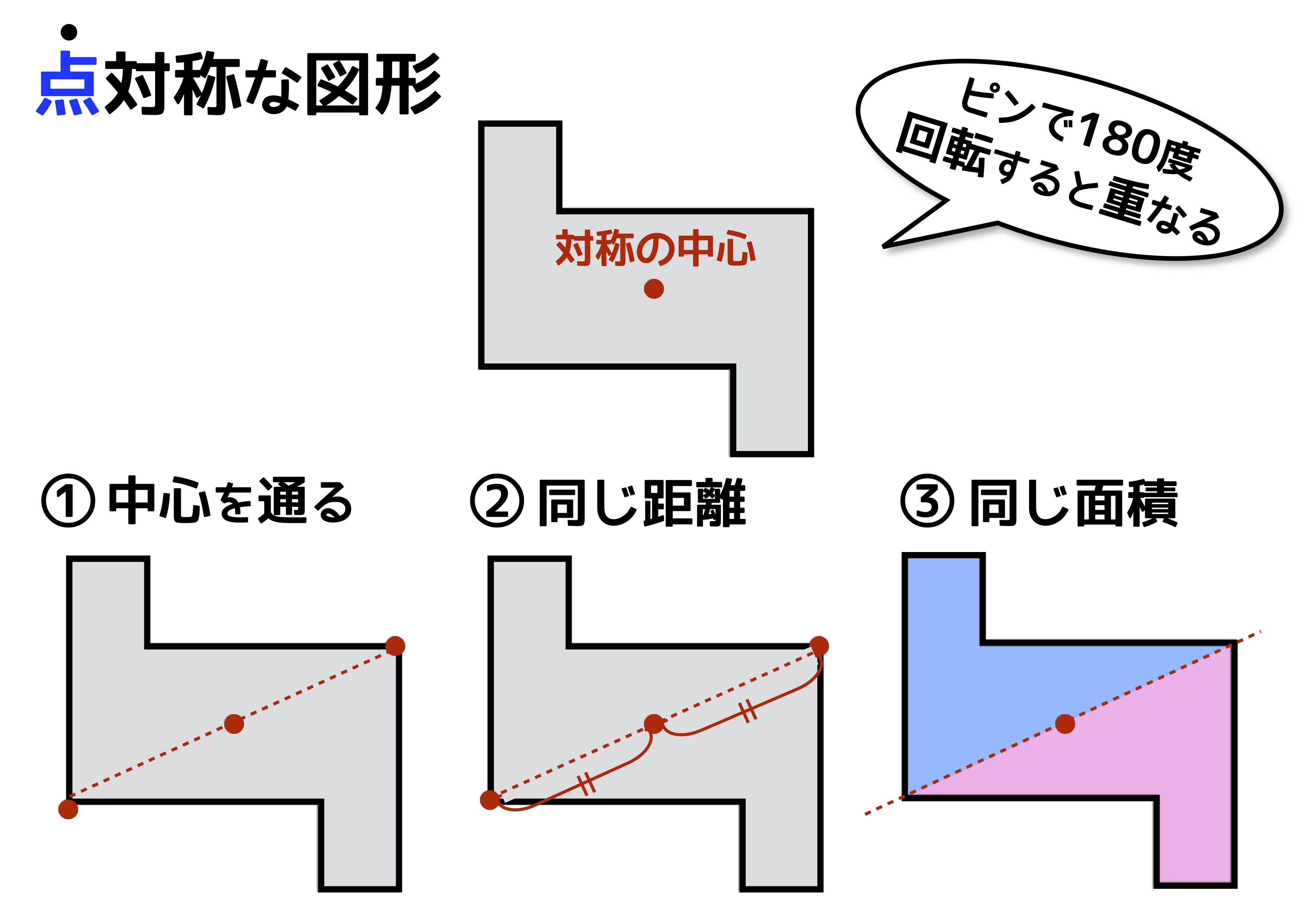



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
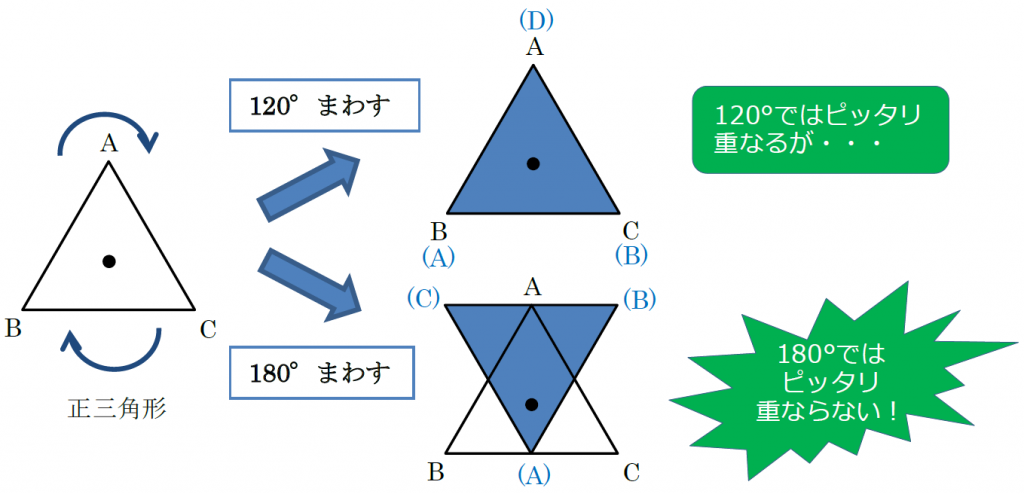



対称 Japaneseclass Jp
対称な図形 線対称な図形 点対称な図形 円の面積 円の面積 角柱と円柱の体積 角柱と円柱の体積 拡大図と縮図 拡大図と縮図1 拡大図と縮図のかき方 1 線対称と点対称を記号で表す。 2図形の対称をつくるには 点を先に対称移動させる。 (対称を記号であらわす) 対称に書いた点と点を結ぶ。 そして 「図形は点の集まりである」誰か助け 算数 小学生 約4年前 🌸アロンアルファ(ゆなりん)🌸 点対称の書き方がわかりません!!



Math 点対称な図形のかき方 働きアリ



6年算数対称な図形2 正多角形教え方
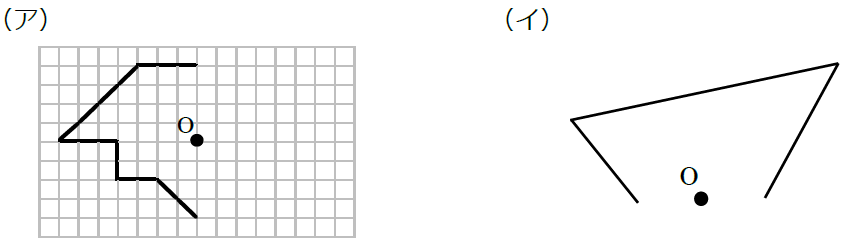
点対称な図形 点対称な図形 → 印刷用PDFは別頁 点対称な図形では,次の図のように1つの点から対称の中心を突き抜けて向こう側に同じ距離だけ進むと対応する点があります。 それぞれの点に対応する点があります。 ※ 花火のように広がる図形・放射状 点対称な図形のかき方がわかりません。 進研ゼミからの回答 点対称な図形の対応する点は,頂点から対称の中心を通る半直線をひき,中心までの距離が等しくなるようにとります。 点対称では,対称の中心は,対応する2線対称、点対称な図形の書き方中学1年数学 Step1まずノーヒントで解いてみよう! Step2正解か? 理解しているかチェックしよう! Step3疑問点があれば、授業動画を見よう! If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the



小6算数 対称な図形 指導アイデア みんなの教育技術



中学数学 線対称な図形 中学数学の無料オンライン学習サイトchu Su
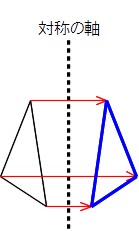
(例)点対称な図形も、ぴったりと重なるので合な図形と関係していると思う。対応す る点や辺の見つけ方はどうなるのか知りたい。対角線が関係しているような気がす る! 対称な図形no5 ~点対称~点対称な図形の書き方その1 中心点や対応する点や線に気づかせます。また、定規やコンパスの使い方を聞かれた時は教えます。 点対称図形の書き方 対称の中心が図形の辺にある場合 ↓ 動画作成協力・・動くイラストフリー素材 点対称な図形の書き方その2 点対称移動後の三角形a'b'c'とすれば、 線分aa'、bb'、cc'には必ず「回転の中心o」がふくまれているんだ。 この性質を使ってガンガン点対称移動させまくろう!! 5ステップで完成!? 点対称移動の書き方・作図方法 それじゃあ、点対称移動の書き



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html



Math 点対称な図形のかき方 働きアリ
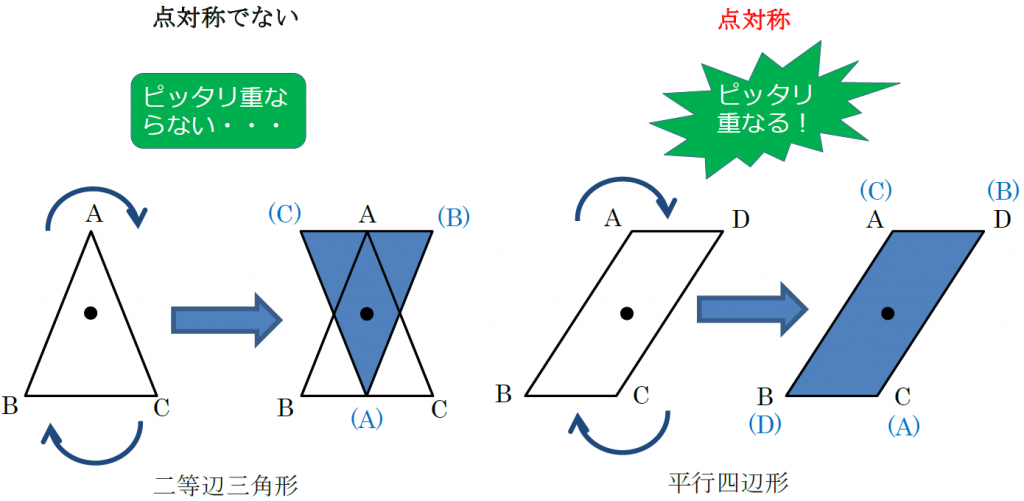
点対称な図形を作るための条件! ①対応する点を結ぶ直線は対称の中心 を通る。 ②対称の中心から対応する点までの長さ は等しくなっている。 つまり,この画像では点Aからの直線は 対称の中心を通っているので,点Oから 下の手順で見分けてみましょう。 ①図形に縦線を入れる ↓ ②図形を180度回転させる (①でできた、直線と図形の交点を上から下まで回して移動するイメージ) →180度回転させたときに元の図形と同じ形になれば「点対称」 →180度回転させる間に左右が同じ形になるときがあれば「線対称」 (左右対称になる回数=対称軸になる・分子内の化学結合は軌道の対称性に大きく規制されている 対称性が一致しないと結合形成できない 分子軌道 対称性 定性的な解釈 波動関数(を用いた量子力学計算)定量的な解釈 例 水分子形状を分析して、その対称性分類したい(=点群の決定) 方法
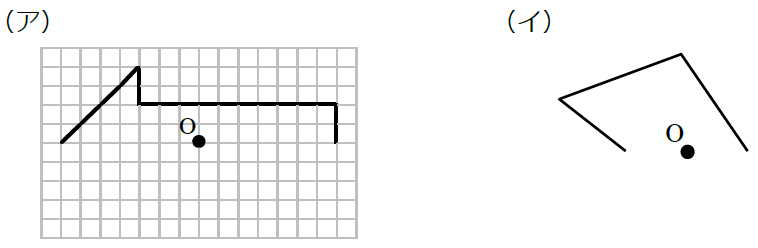



中1数学 点対称な図形とは まなビタミン
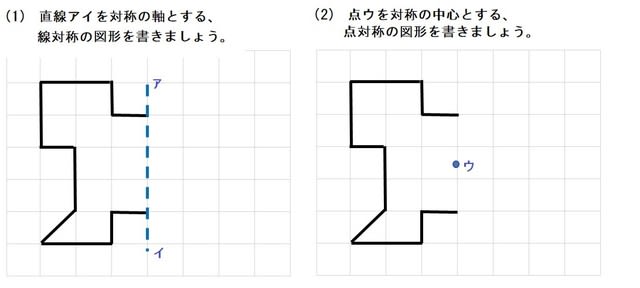



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support




6年算数 対称な図形 指導実践 点対称のかき方のコツ ネコ好きな学校の先生の日常



点対称の簡単な書き方を教えてください 逆さまにした時に同じに見えるこ Yahoo 知恵袋
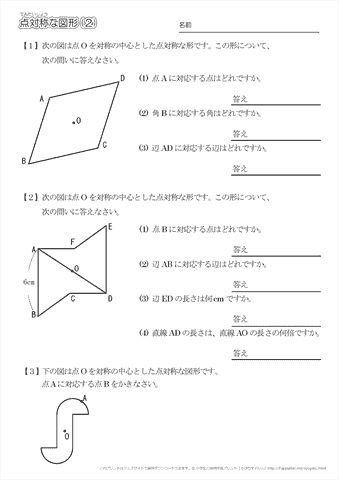



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生




世界一分かりやすい算数 小6 対称な図形



1
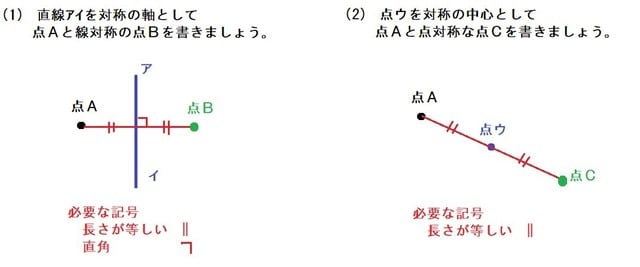



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support
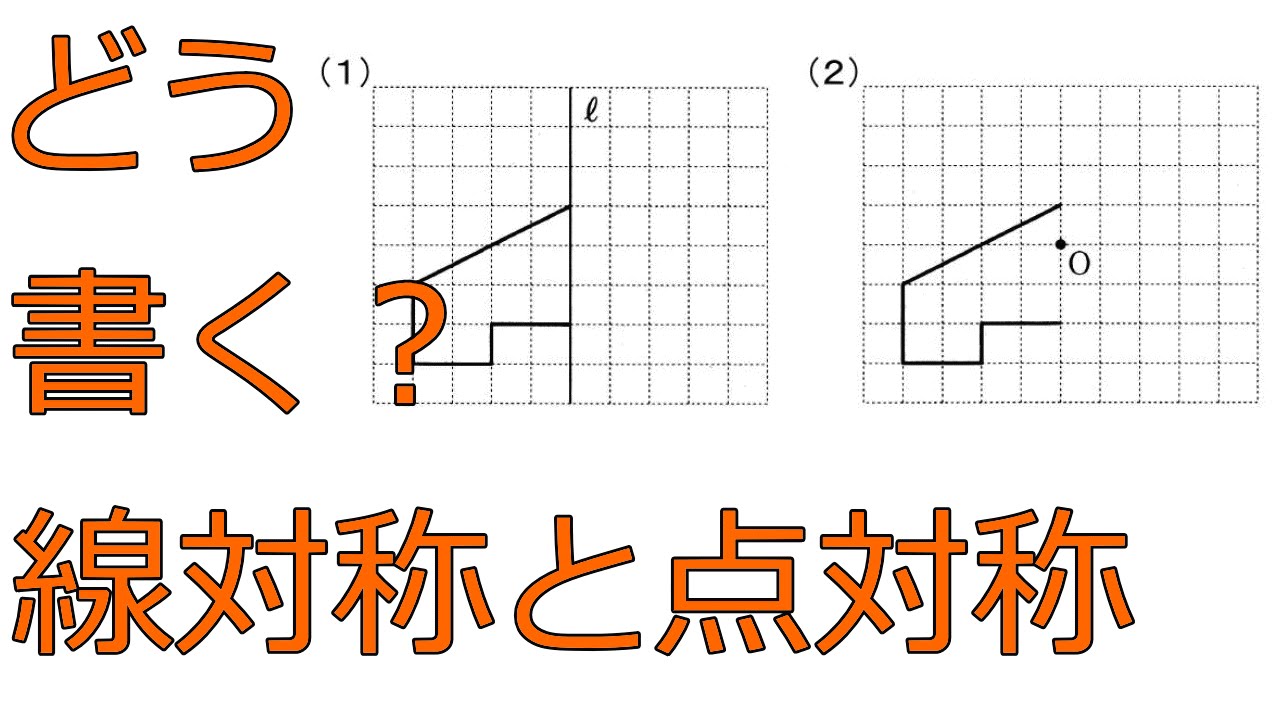



線対称 点対称な図形の書き方 中学1年数学 Youtube
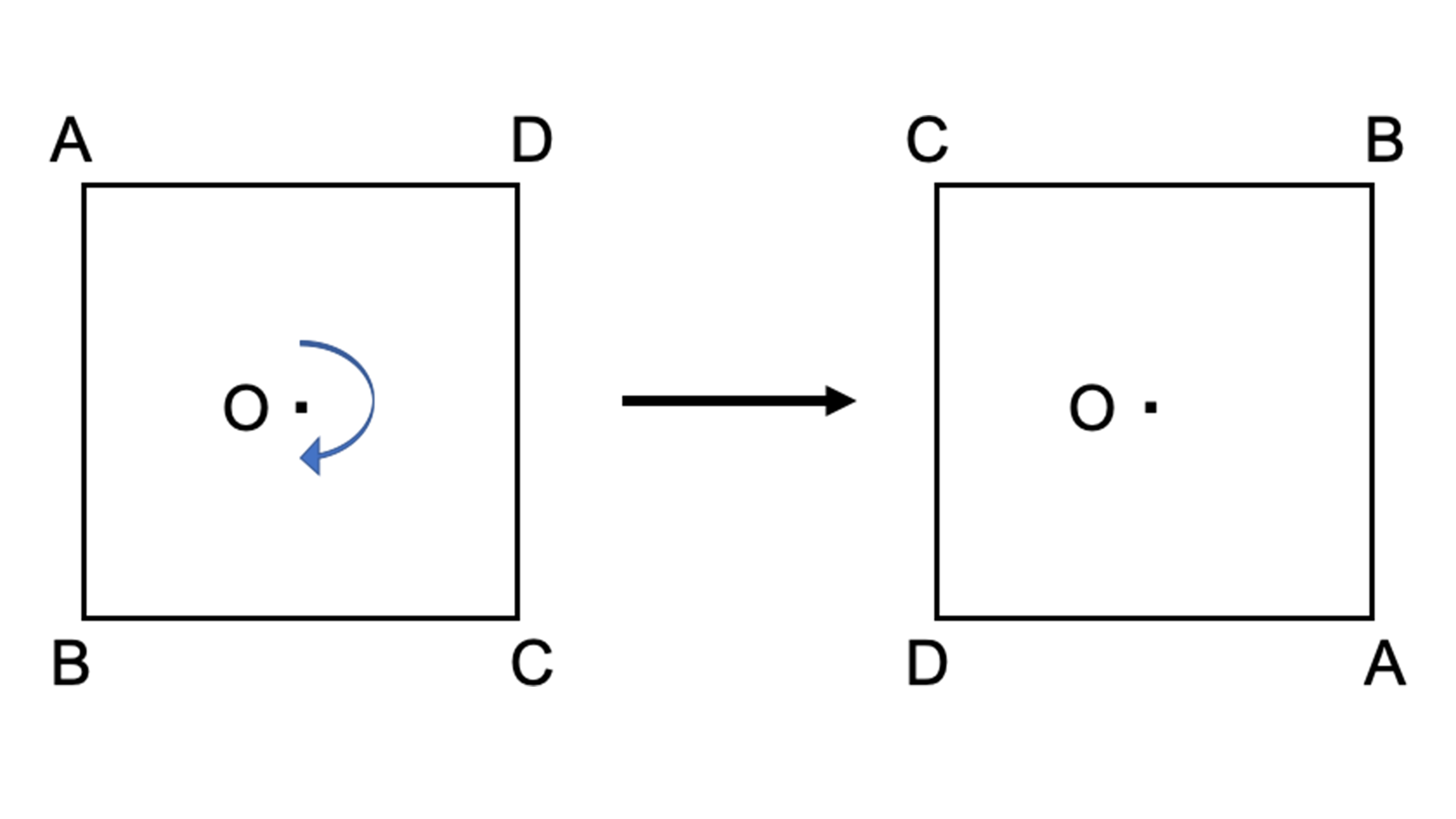



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



Http Www Edu City Yokohama Lg Jp School Es Kamisueyoshi Index Cfm 1 2178 C Html 2178 0525 Pdf
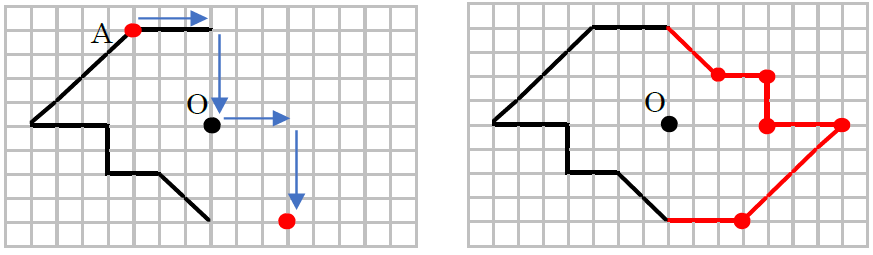



中1数学 点対称な図形とは まなビタミン




対称の中心を使わずに点対称な図形をかく 算数を究める



1



最新の記事 翁島 おきなしま 小学校ホームページ
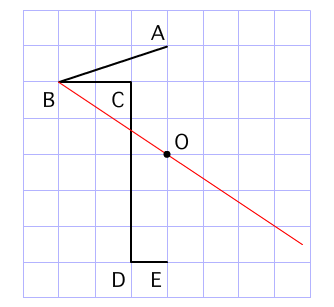



Tossランド 点対称な図形 作図




点対称な図形はコンパスでかける 小6向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス



最新の記事 翁島 おきなしま 小学校ホームページ




悩みのタネ 解決編 線対称と点対称 声に出さないけど思っていること




点対称の図形の書き方を教えてください Clear



平面図形 点対称な図形のかき方 中学数学 定期テスト対策サイト




線対称の作図 4つのステップでわかる 対称移動の書き方 Qikeru 学びを楽しくわかりやすく



Http Www Magokoro Ed Jp Inaridai2 E Manage Contents Upload 5ebb39a3b1bdd Pdf




スマホok 6年 対称な図形 点対称な図形のかき方 Youtube



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support




Tossランド 点対称な図形 作図



Http Cms Nerima Tky Ed Jp Weblog Files 103 Doc Pdf




Primary算数的対称な図形 筆記 Clear



中1数学 点対称な図形とは まなビタミン



1



点対称な図形




小6算数 対称な図形 点対象 指導アイデア みんなの教育技術



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support




対称な図形 線対称と点対称 小学生 算数のノート Clear



中1数学 点対称な図形とは まなビタミン



スマホok 6年 対称な図形 点対称な図形のかき方 Youtube




対称な図形 線対称と点対称 小学生 算数のノート Clear
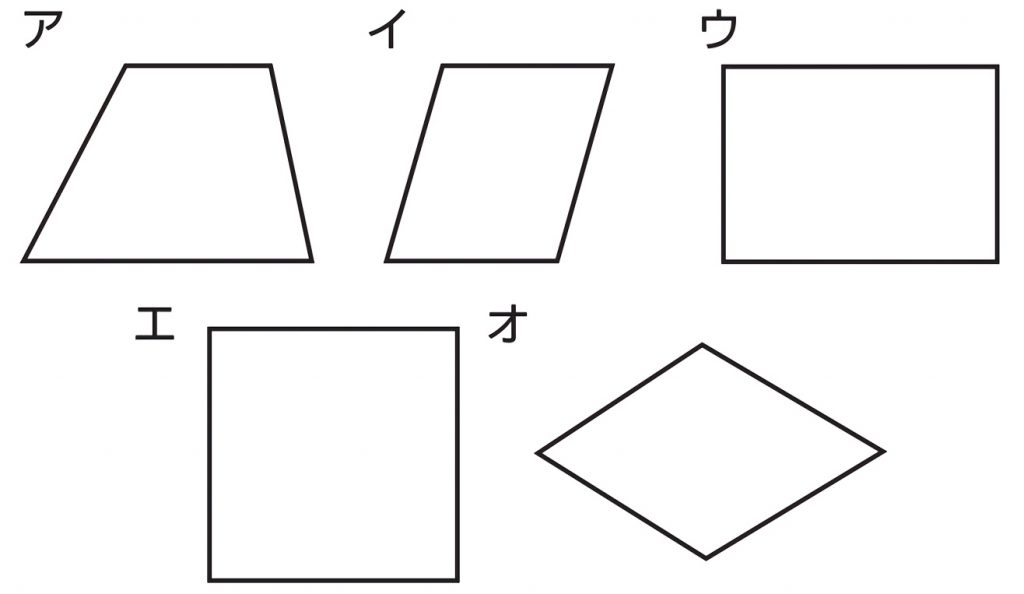



小6算数 多角形と対称 指導アイデア みんなの教育技術



Math 点対称な図形のかき方 働きアリ The 2nd




対称の中心を使わずに点対称な図形をかく 算数を究める



Studydoctor点対称とは その性質 中学1年数学 Studydoctor




点対称な図形を書く




世界一分かりやすい算数 小6 対称な図形



点対称な図形のかき方2 スクールプレゼンター教材共有サイト スクプレ道場



中1数学 点対称な図形とは まなビタミン
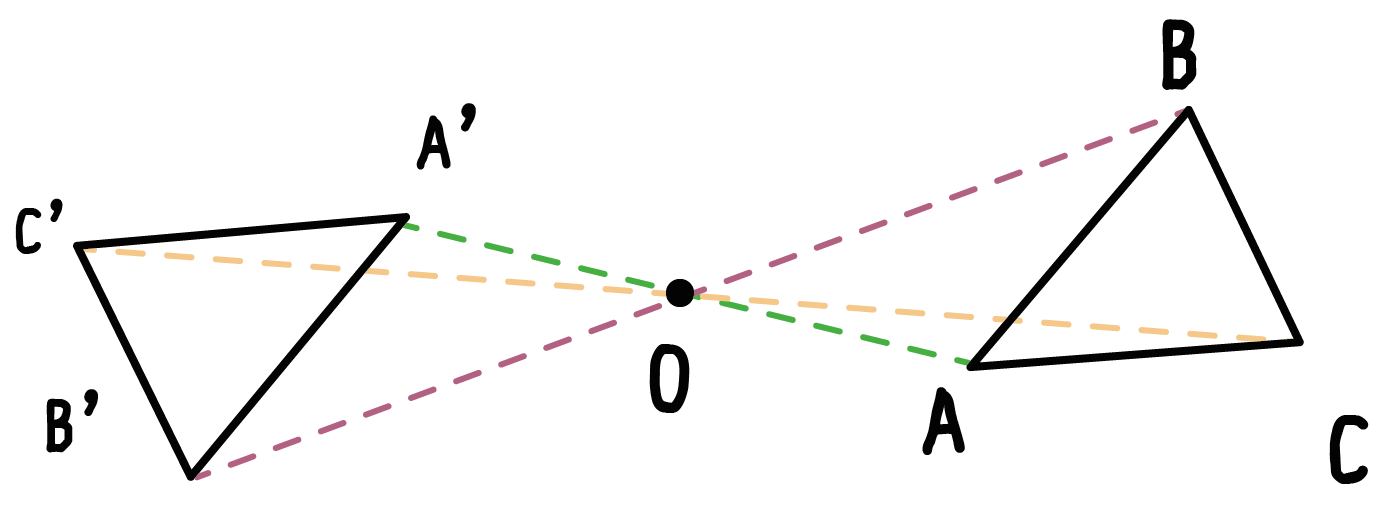



平面図形 5ステップでできる 点対称移動の作図 書き方 Qikeru 学びを楽しくわかりやすく
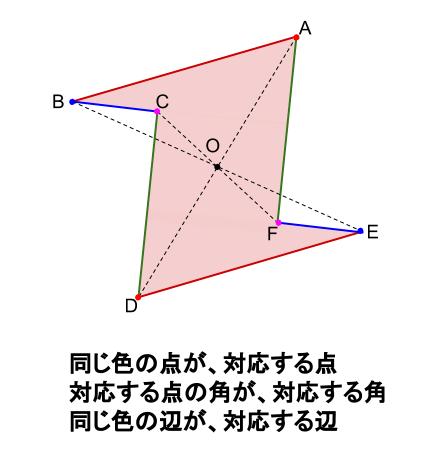



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su



この点対称の書き方教えてください 図のように各頂点とo Yahoo 知恵袋




線対称の作図 4つのステップでわかる 対称移動の書き方 Qikeru 学びを楽しくわかりやすく
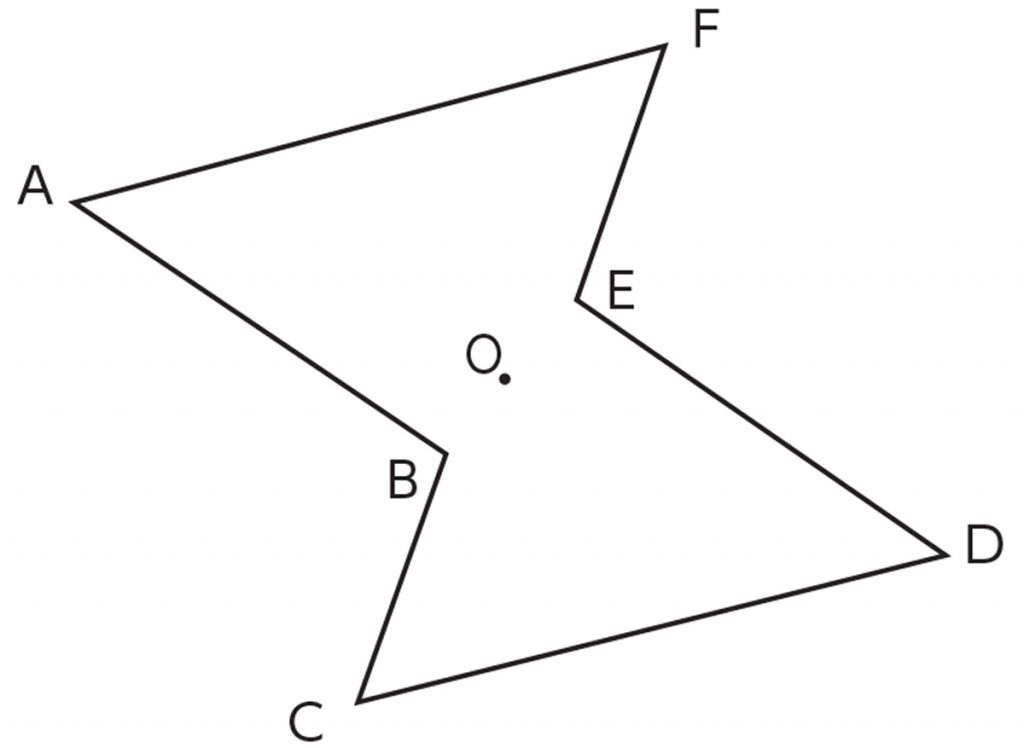



小6算数 点対称な図形の性質 指導アイデア みんなの教育技術




線対称 点対称な図形のかき方 対称な図形 小6算数 豊橋の学習塾 勉強 Youtube スタディチューブ
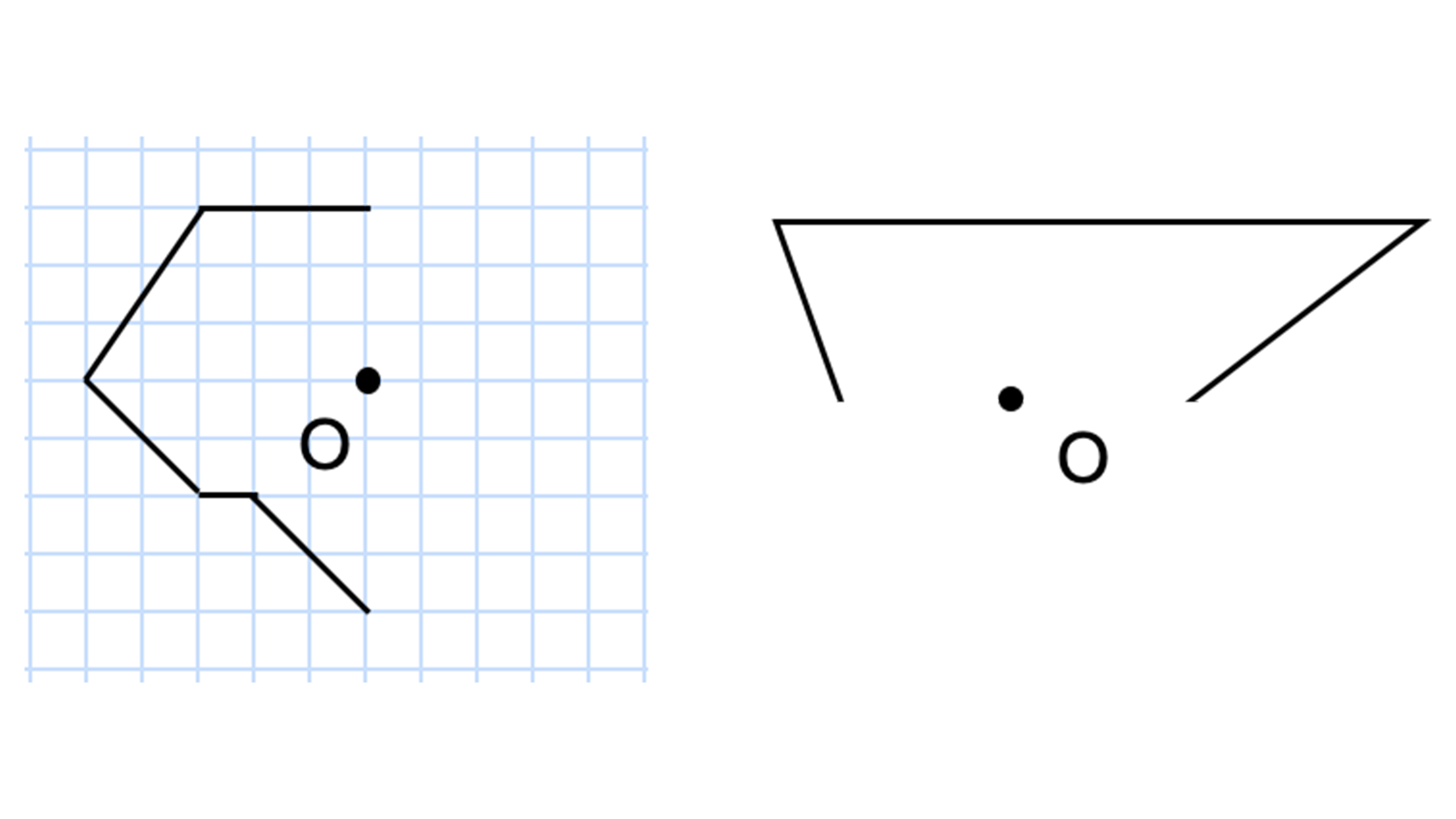



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




6年算数 対称な図形 指導実践 点対称のかき方のコツ ネコ好きな学校の先生の日常
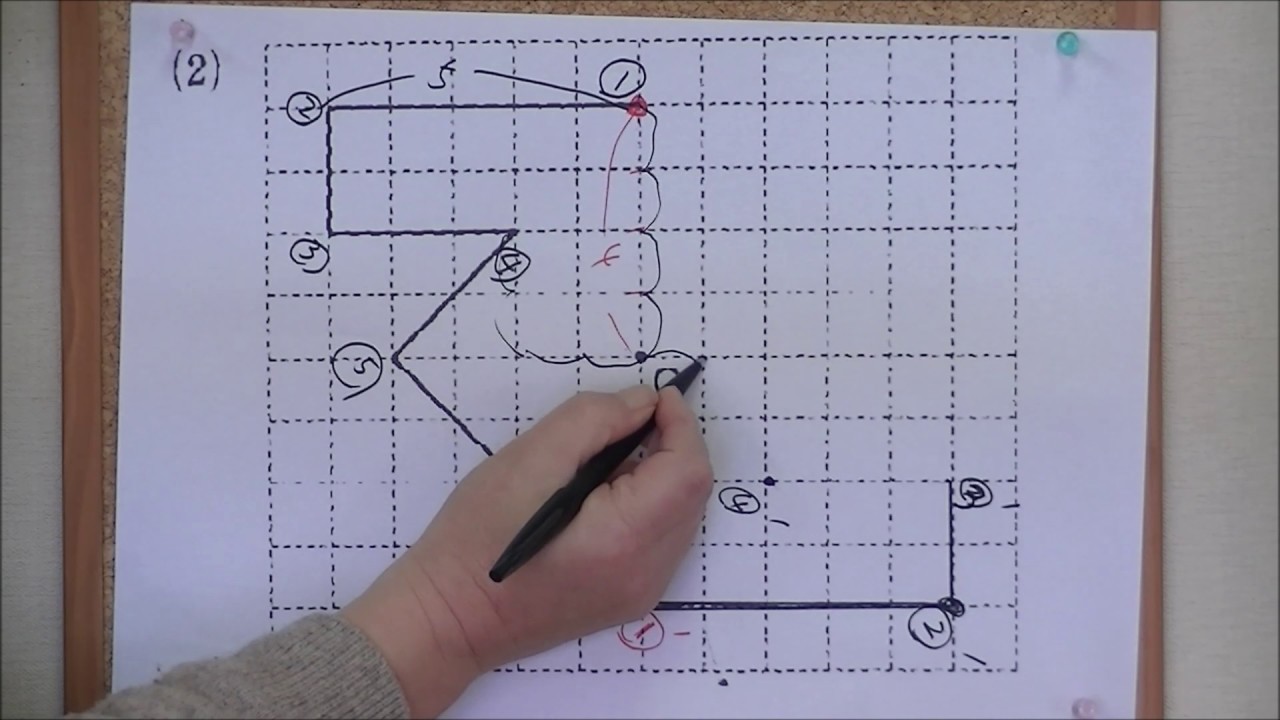



小学6年算数 点対称な図形の描き方 Youtube
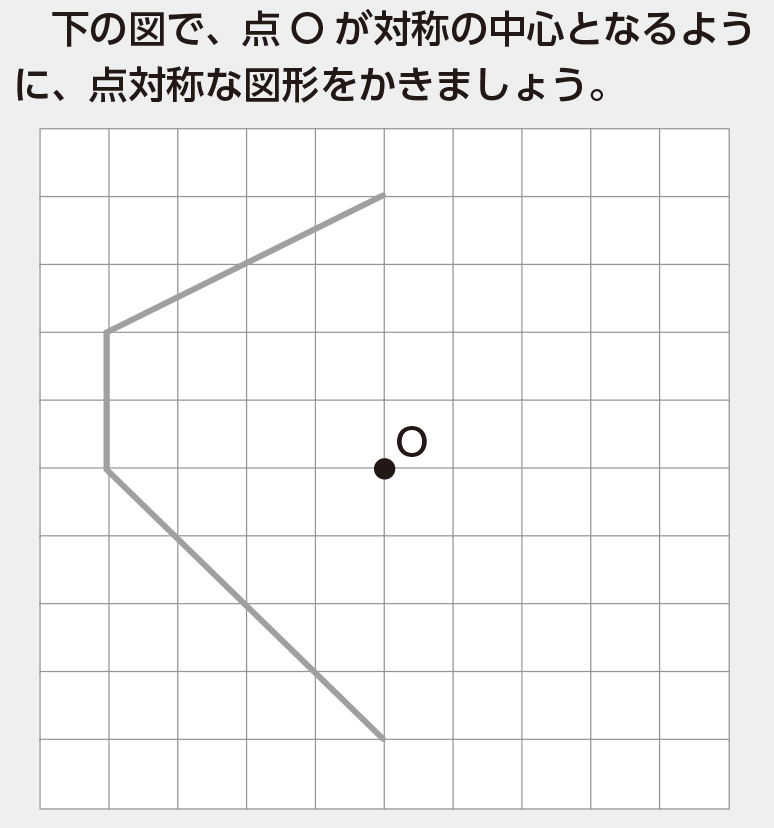



小6算数 対称な図形 点対象 指導アイデア みんなの教育技術




図形の対称移動の作図手順と性質 数学fun
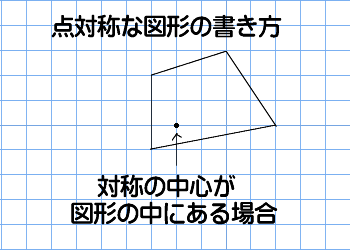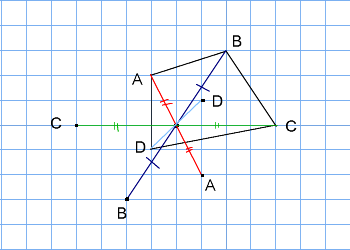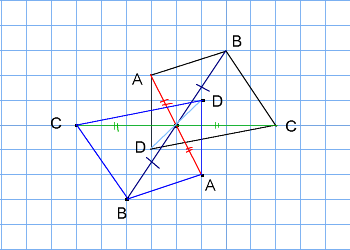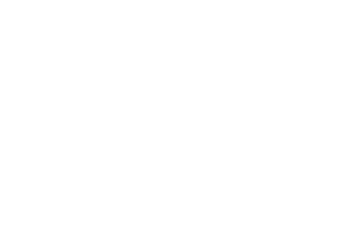



6年算数線対称点対称図形 わかる教え方
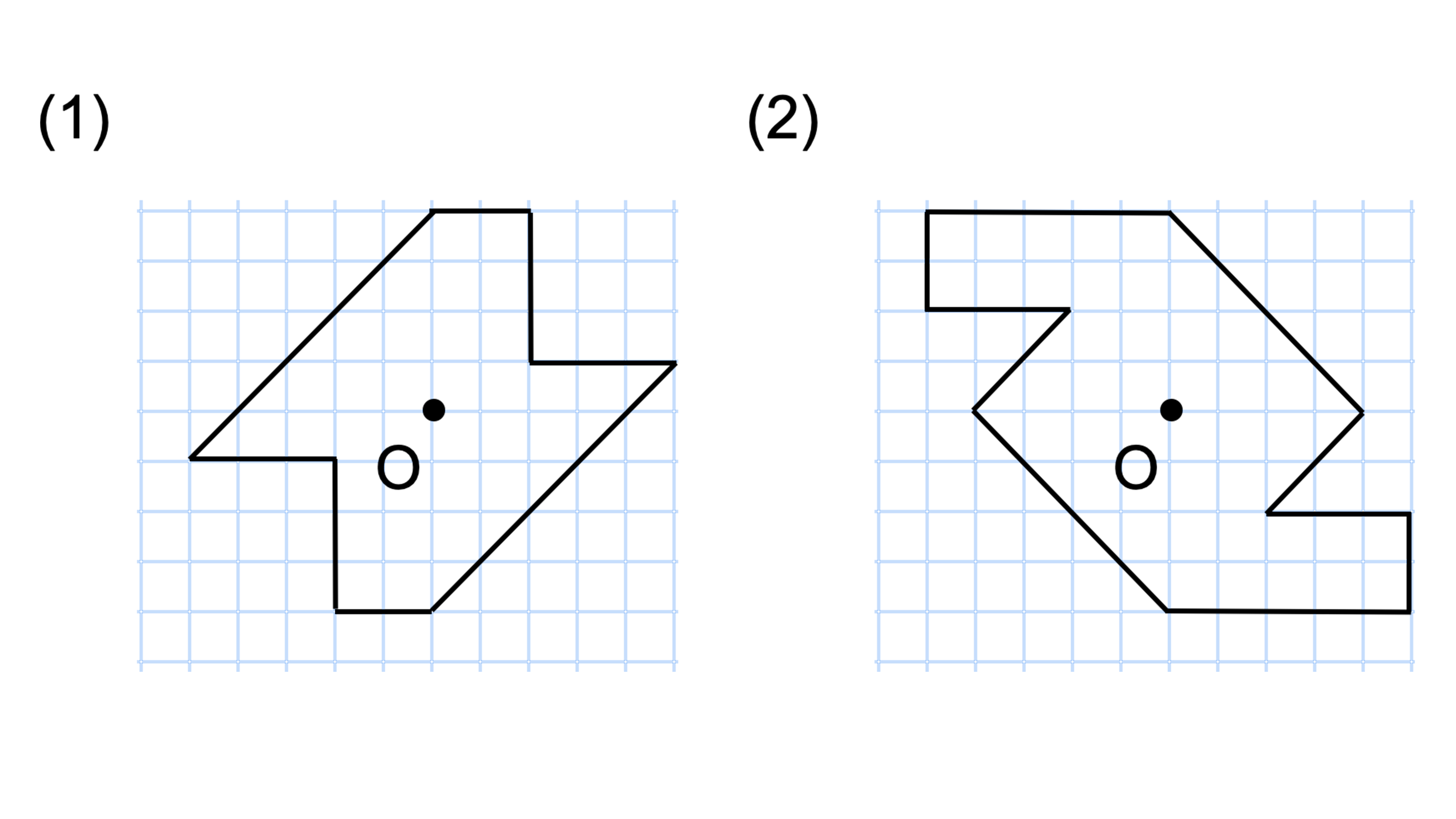



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
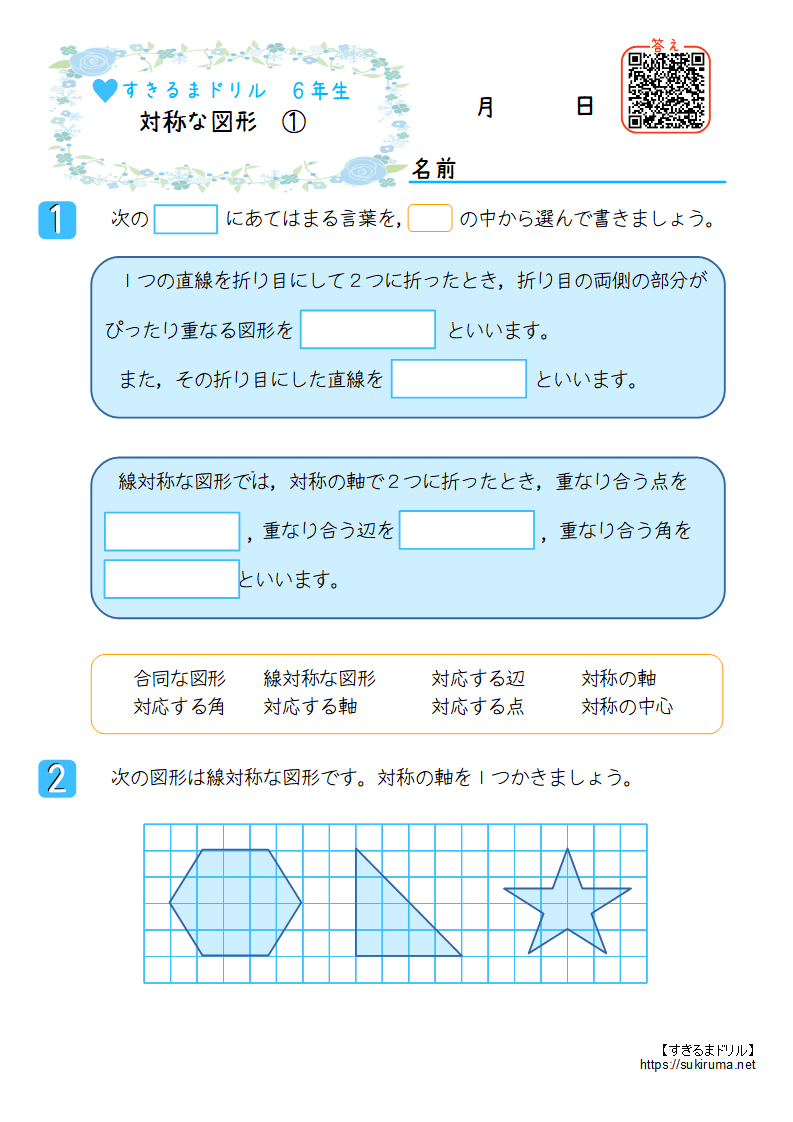



すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 無料学習プリント



点対称な図形のかき方 Youtube
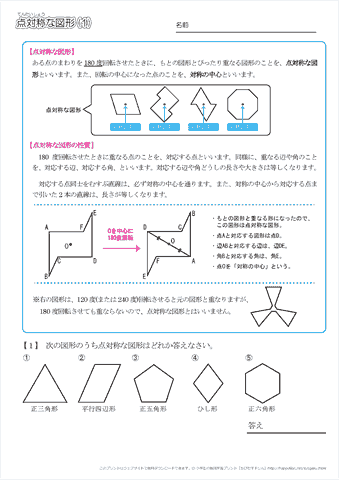



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生




โน ตของ 小六の復習 線対称 点対称な図形 ช น Primary算数 Clear



Http Www Edu City Yokohama Lg Jp School Es Kamisueyoshi Index Cfm 1 2178 C Html 2178 0525 Pdf
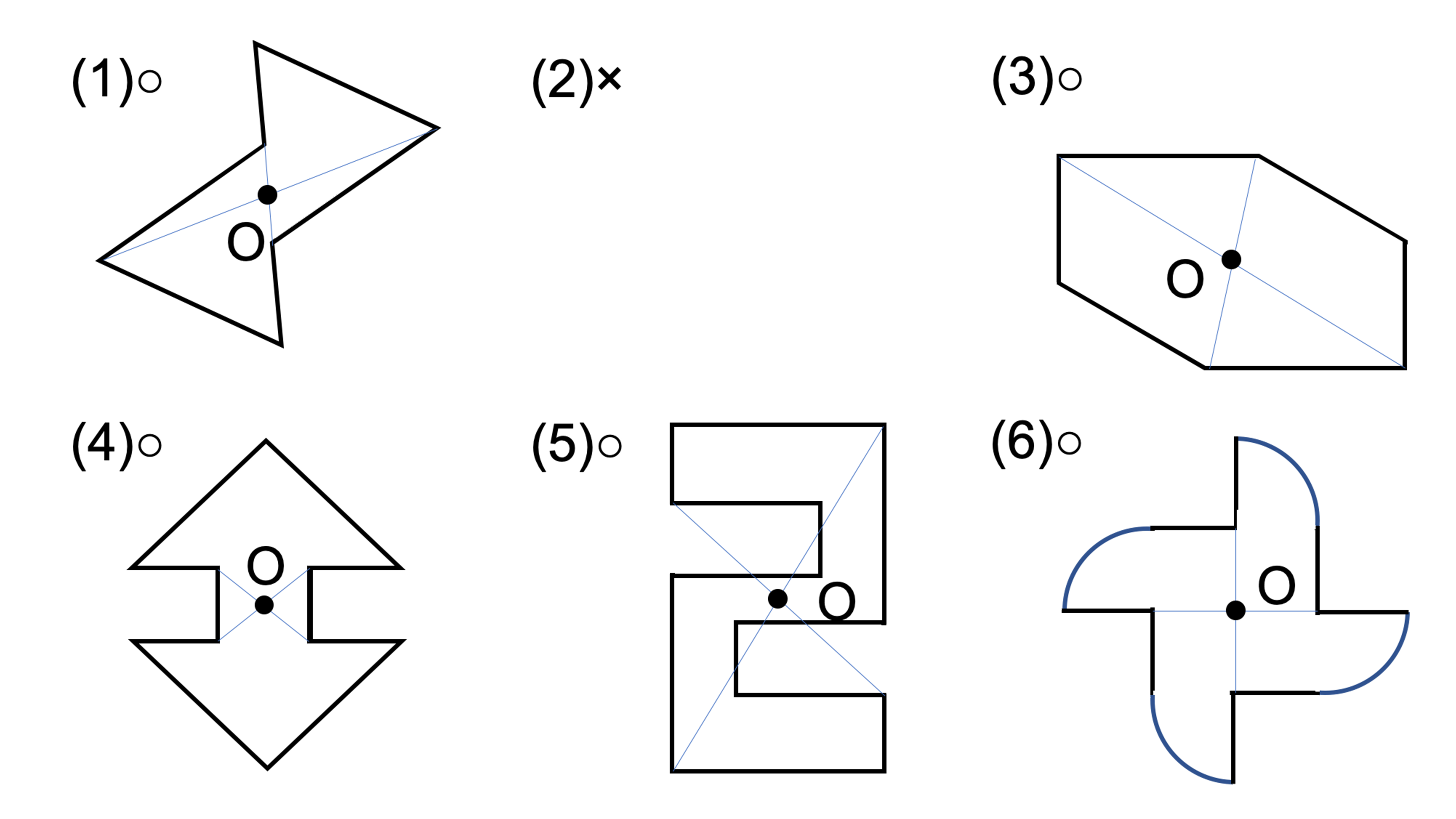



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
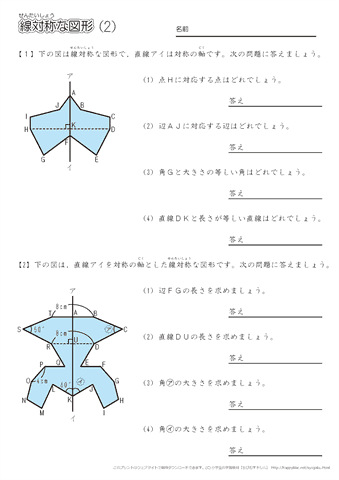



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生
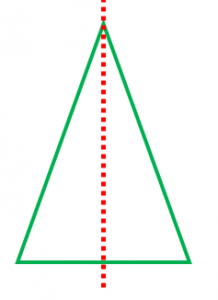



対称の軸 線対称の意味と 正多角形などでの本数 具体例で学ぶ数学




対称の中心を使わずに点対称な図形をかく 算数を究める
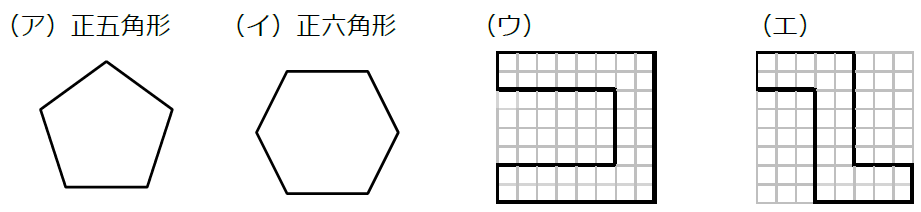



中1数学 点対称な図形とは まなビタミン




線対称 点対称 算数用語集




点対称移動 Youtube




6年 線対称 点対称 小学生 算数のノート Clear



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html




線対称 点対称 算数用語集
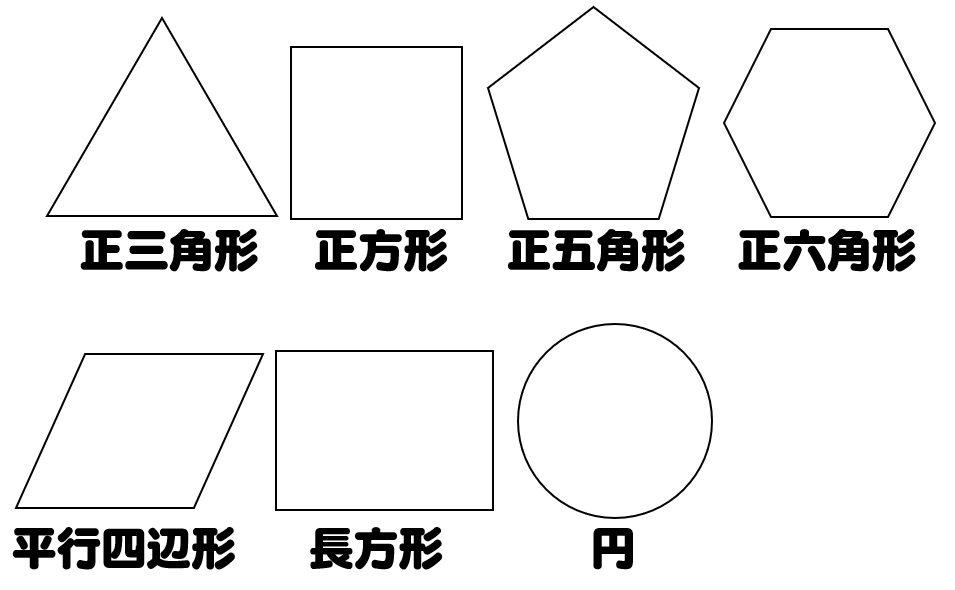



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun
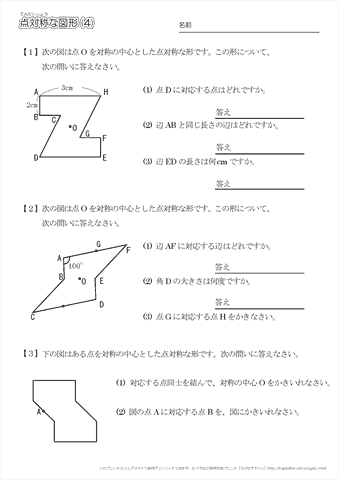



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
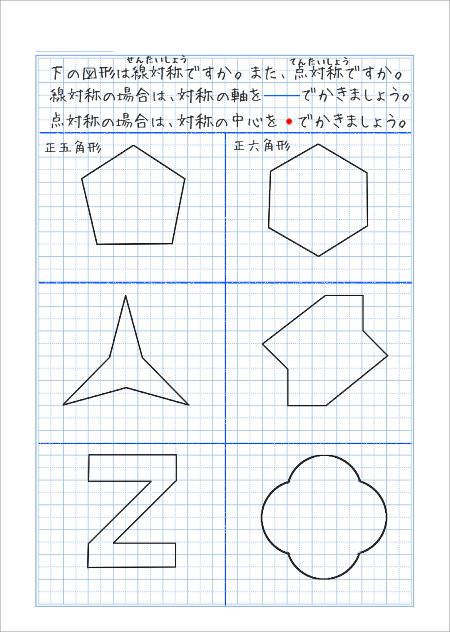



線対称と点対称の自主学習ノート 家庭学習レシピ



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html




線対称の作図 4つのステップでわかる 対称移動の書き方 Qikeru 学びを楽しくわかりやすく




6年算数対称な図形2 正多角形教え方
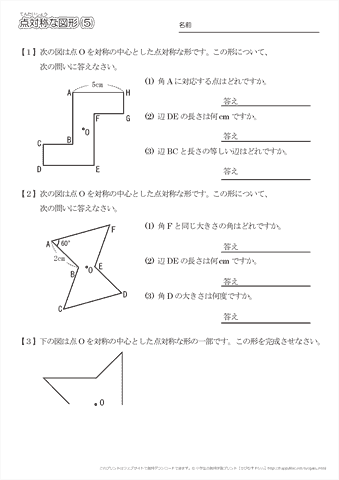



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生



Math 点対称な図形のかき方 働きアリ
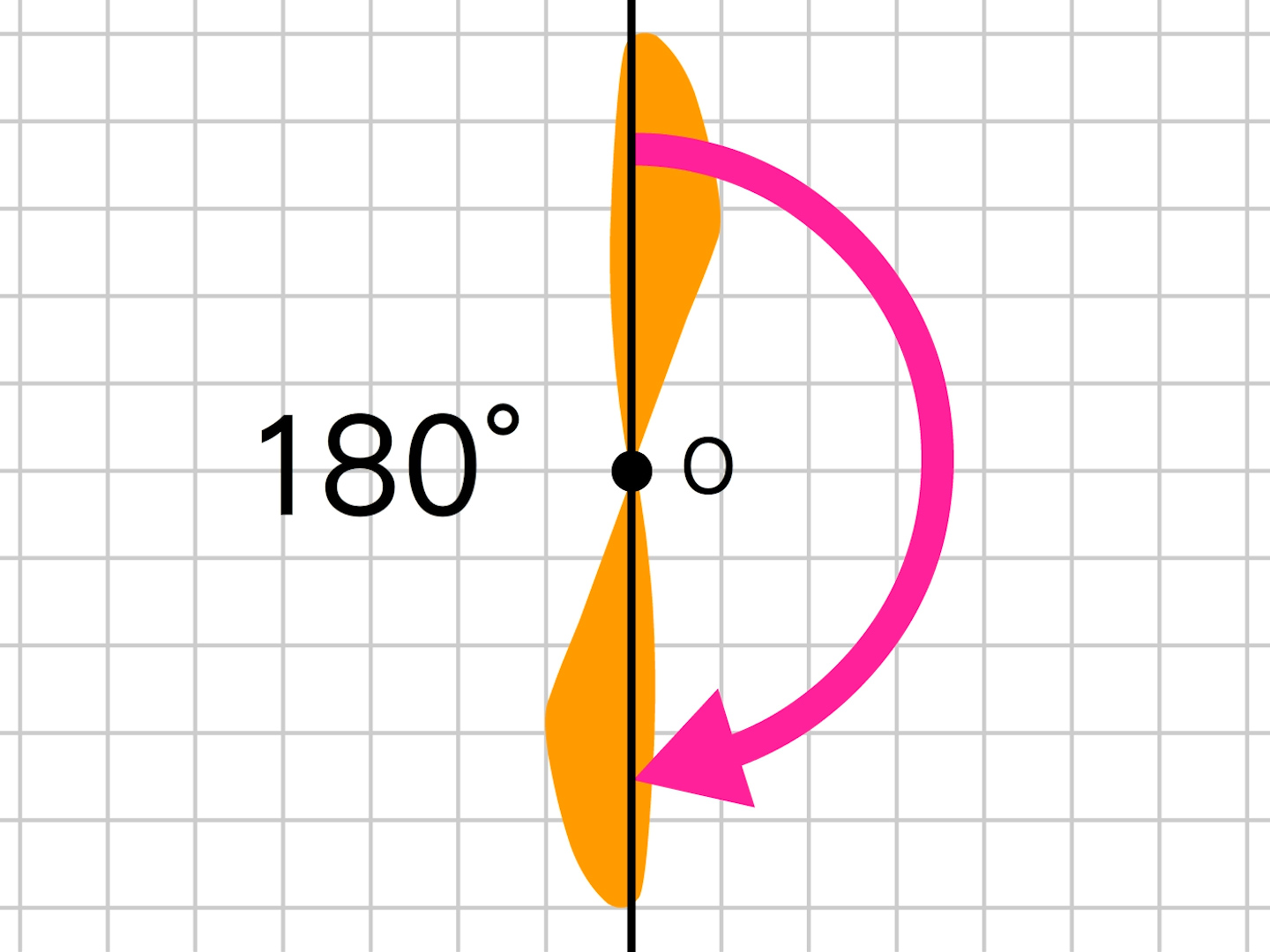



6年 点対称な図形 算数イメージ動画集 大日本図書
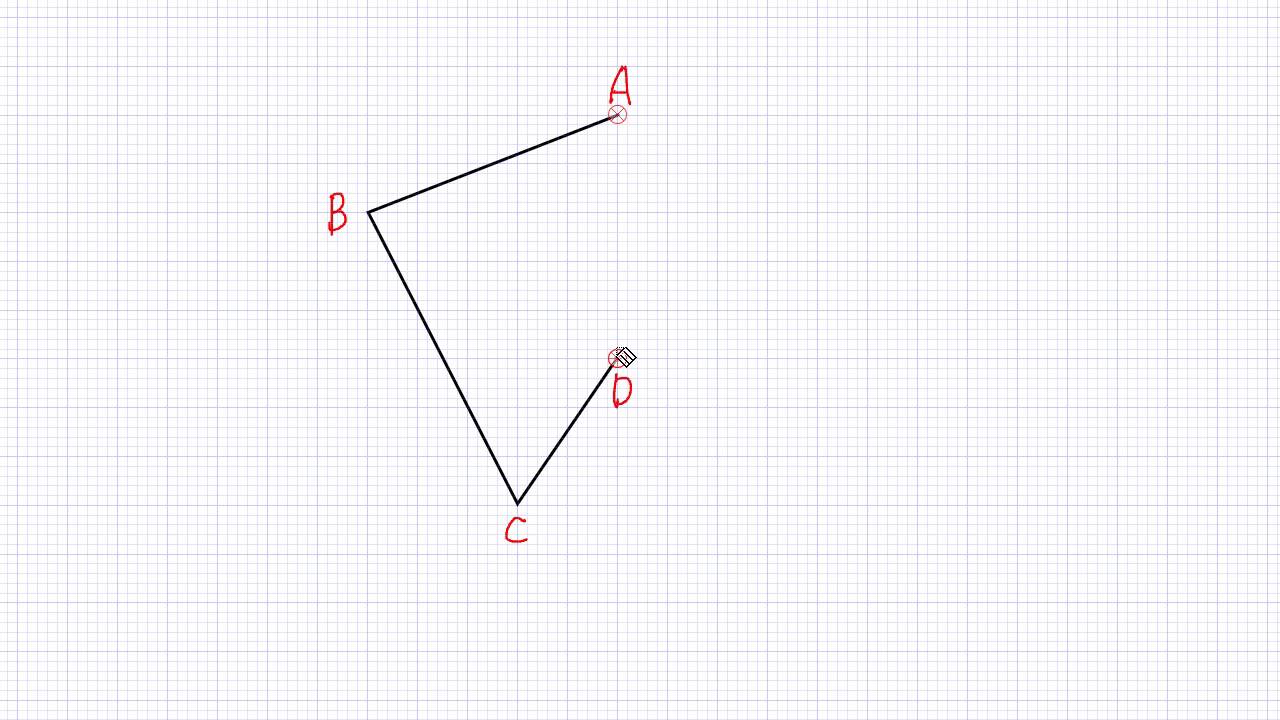



点対称な図形のかき方 Youtube
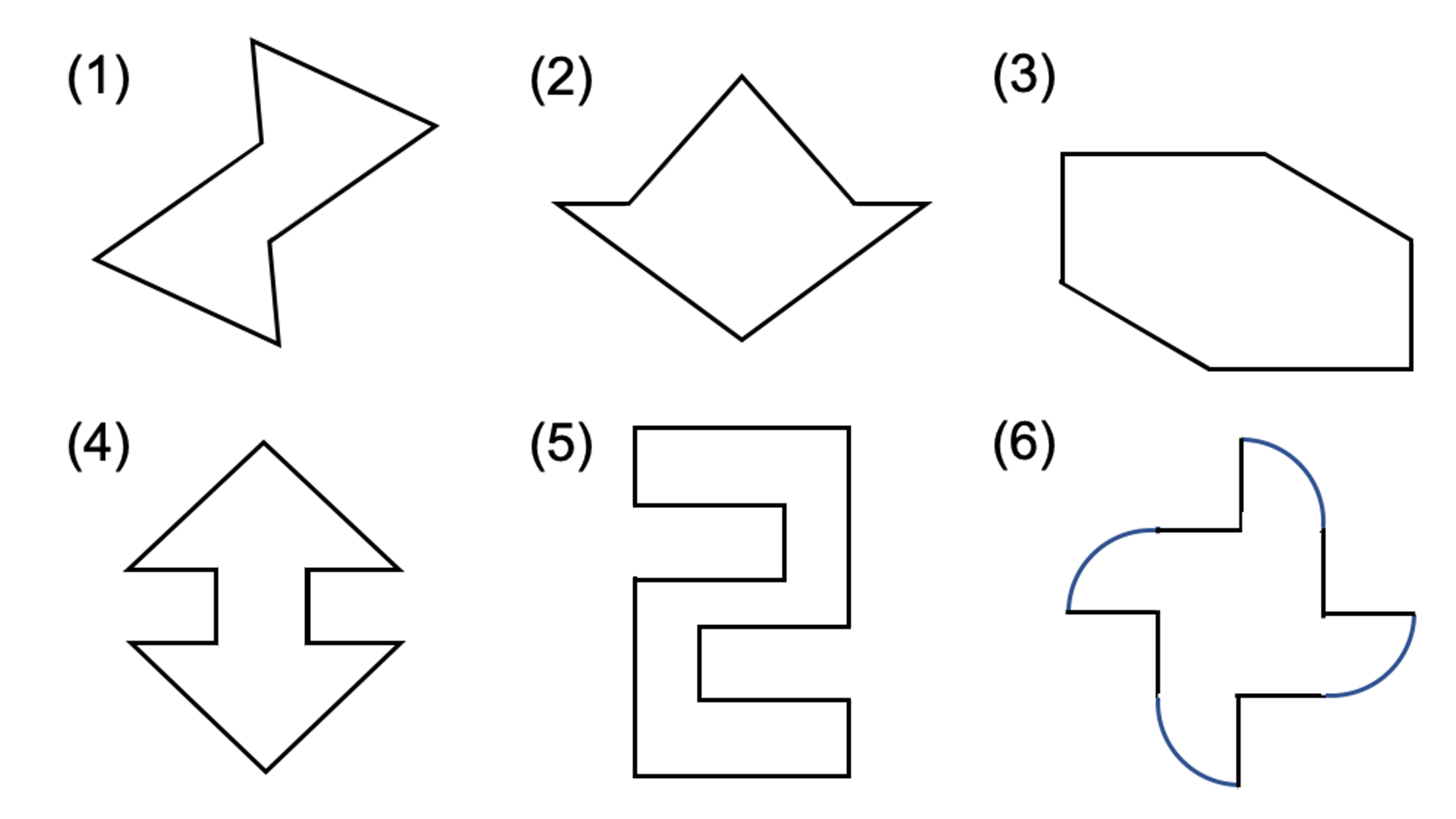



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
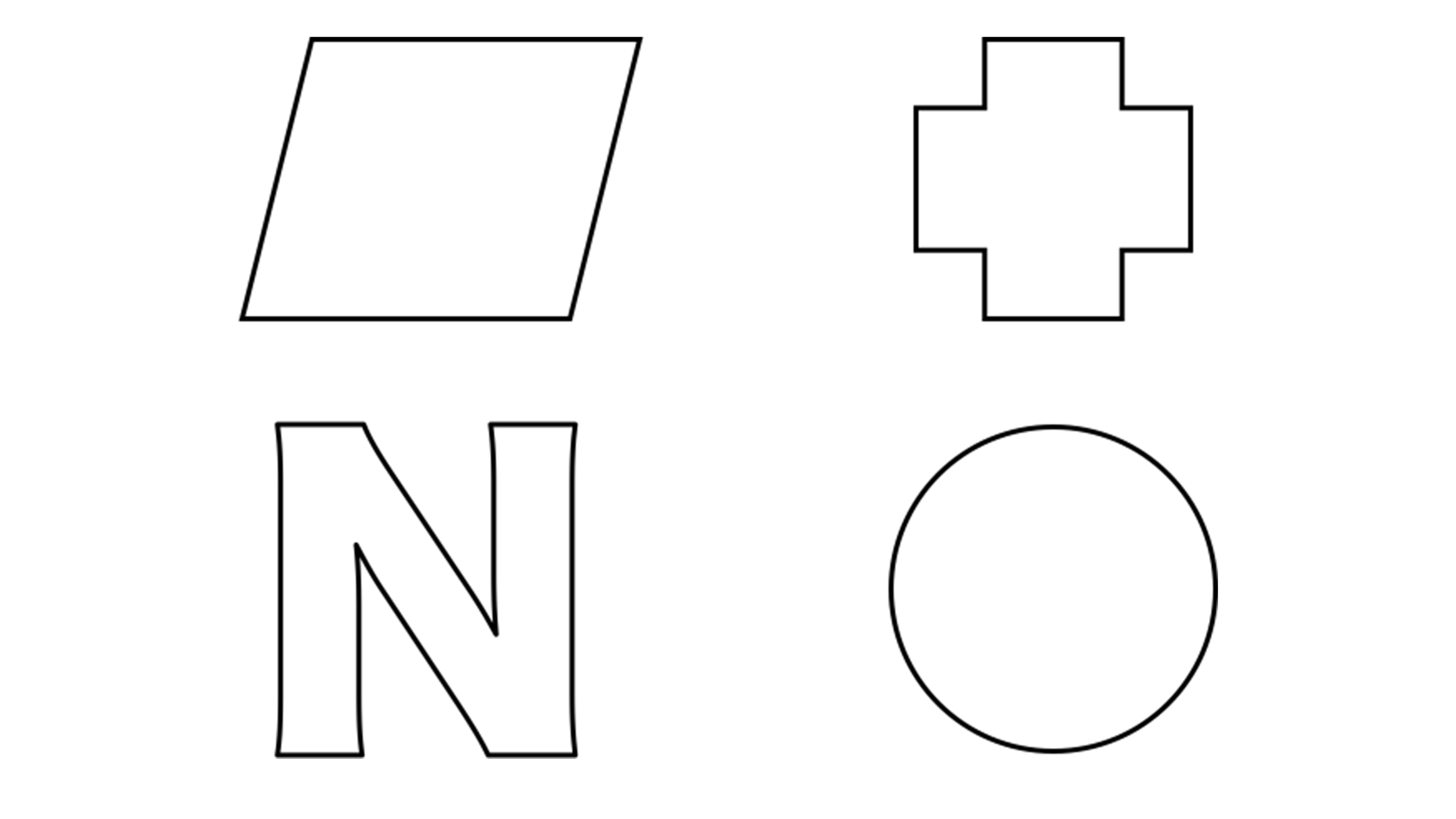



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



小6です この点対称の書き方がわかりません 助けてください Yahoo 知恵袋
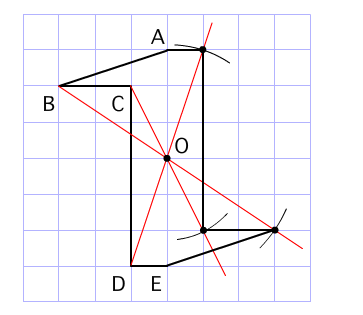



Tossランド 点対称な図形 作図



0 件のコメント:
コメントを投稿