単な角錐と円錐の体積を求めることを学習する。このとき,底 面積と高さを測定し,それらを用いた計算によって立体の体積 を求める。なお,角錐や円錐の体積については,同底,等高の 角柱や円柱の体積と比較させ,その1/3に等しいことを実験,実 三角錐の表面積の求め方の公式 次は三角錐の表面積を求める公式です。 すると、今回の三角錐は以下のように展開することができます。 ゴートゥーイート 11月中に終了する可能性高いですか?キャンペーンに気付いてなくて最近予約し始めたので 今回は1.三角錐の体積の求め方 11三角錐 四角錐台の体積を計算する必要がありました。 上記公式に数字を当てはめるとA=43 B=36 a=29 b=19 h=18 単位cmです。 公式に当てはめて計算してみると大方18リットル=10升=?斗であることがわかりました。

立体几何中与锥体体积有关问题的求解策略 雪花新闻
三角錐 体積 証明 積分
三角錐 体積 証明 積分-こんにちは。相城です。今回は三角錐を2つに分けたときの頂点を含む部分と,もとの三角錐との体積比の公式の紹介と証明を行ってみたいと思います。 三角錐に関する公式 下の図の三角錐で, 三角錐a-dpeと三角錐a-bqcの 空間ベクトルの練習問題です。② 円柱と円錐,四角柱と四角錐の体積の関係 から,同じ底面積で同じ高さをもつ他の立体 (五角柱と五角錐など)の体積の関係を類推 する。 ↓ 3 一般化する ③ 同じ底面積で同じ高さをもつ,柱体と錐体 の体積が常に一定の関係にあることを理解 する。 ↓



圆锥体积公式 万图壁纸网
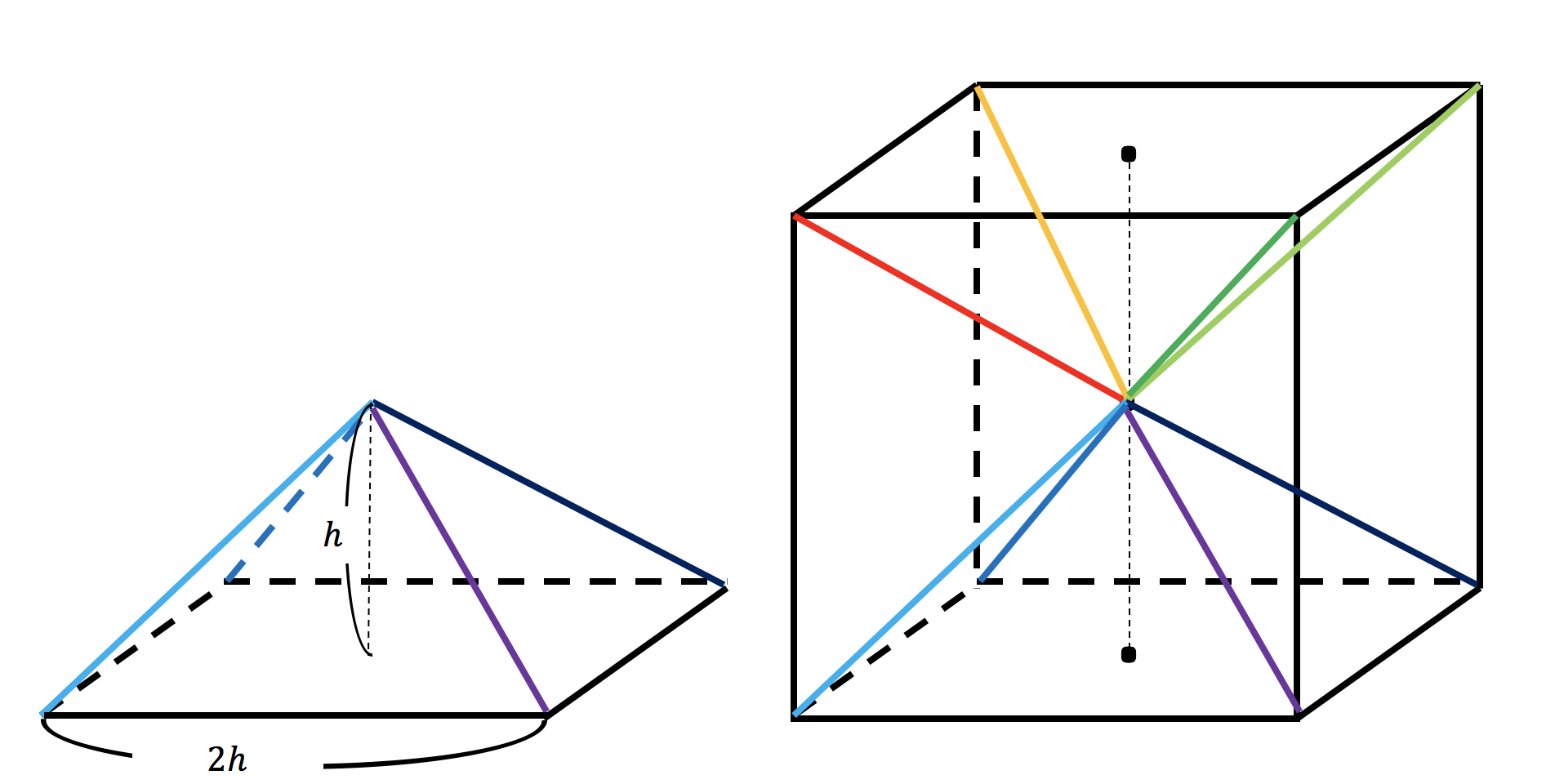
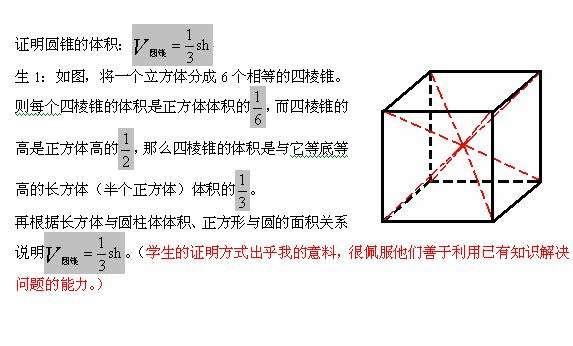
半径r の球の体積は 4 3 ˇr3 であることを学んだ。しかし,中学校の教科書には,これらの事実の証明は書かれ ていない。以下では,円柱の体積の公式と高校の「数学B」までの知識を使って, 円錐の体積の公式を導こう。 x2 円錐の体積すると四角錐kaefj と三角錐kefh に分かれる。 四角錐は台形aefj を底面として高さがak なので (26)×6÷2×2÷3=16 体積16cm 3 三角錐は efh が底面で kから面efghにおろした垂線の長さが高さである。 よって体積は6×6÷2×6÷3=36 よって3616=52 となる三角錐(さんかくすい、英 triangular pyramid, trigonal pyramid )や四面体(しめんたい、英 tetrahedron )とは、垂直断面に三角形を持つ錐体のことである。 辺6本、頂点4つからなる。 面の数は立体に於ける最小限界の4つであることから四面体とも呼ぶ。三角錐は、最小の頂点数で構成するこ
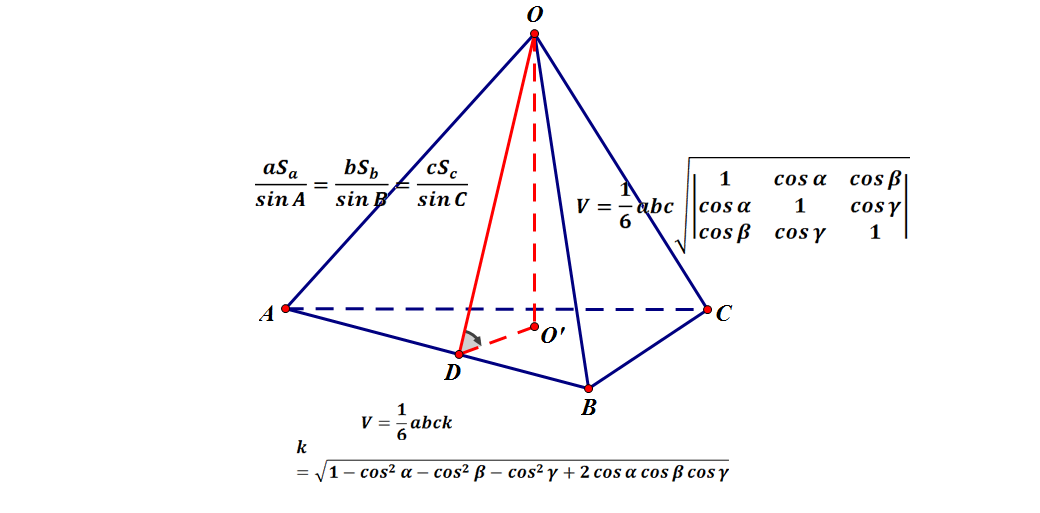
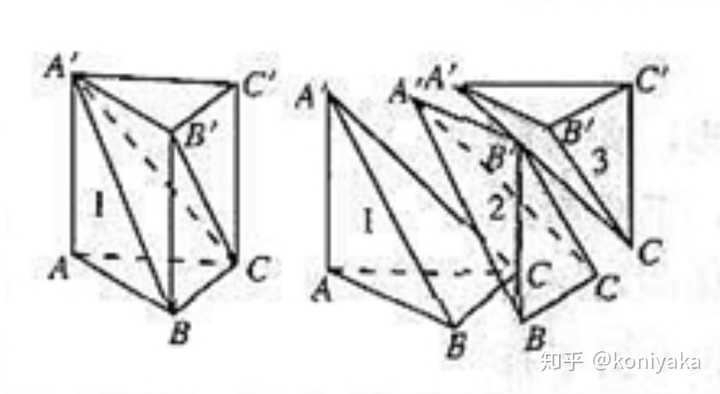
積分を用いた証明 二つ目の説明です 三角錐の体積の求め方 Tweet 三角錐の体積の求め方 解決済 気になる 0 件 質問者: rienomiffy 質問日時: 1810 回答数: 4 件 度々お世話になります。 三角形ABCの3頂点は1つの球の表面上にある。球の半径は2で、球なお,六辺の長さが全て求まっているときには余弦定理により角度( cos \cos cos )が簡単に求まるので,この公式を使えば 六辺の長さから四面体の体積を機械的に求めることもできます。 証明の前に例題です。この公式,一見かなりマニアックですが,意外と検算に使えます。三角錐の体積 三角錐の体積=底面積×高さ× 1 3 証明 三角柱を3つの三角錐に分解することで証明する. (Ⅰ)三角錐 eafc と三角錐 eafd について 三角柱 abcdef の側面 acfd は平行四辺形である. よって ad = cf ・・・・・・(1) ac = df ・・・・・・(2)
こんにちは。相城です。今回は三角錐を2つに分けたときの頂点を含む部分と,もとの三角錐との体積比の公式の紹介と証明を行ってみたいと思います。 三角錐に関する公式 下の図の三角錐で, 三角錐a-dpeと三角錐a-bqcの体積比は になる。 証明 証明 北海道大学 理系 a,bを正の実数とする。 xyz空間内の2点 A(a,0,0),B(0,b,1)を通る直線を lとし、直線lを z 軸のまわりに一回転して得られる曲面をMとする。 1P(x,y,z)を曲面M上の点とする。このとき x,y,zが満たす関係 式を求めよ。 2曲面Mと次の図のようなすべての辺の長さがaの正三角錐(正四面体)ABCDについて考えます。 頂点Aから底面BCDに垂線AHを引くと,このAHの長さが正四面体の高さになります。 このとき,図のように ABHに着目すると直角三角形であるので,三平方の定理を利用してAHの長さを求めることができますが,その前にまずはBHの長さを求める必要があります。 正四面体ABCDを上から




最高50 三角錐体積公式




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ
常に3倍の体積を持つ三角柱(ABC・DEF) を作ることが出来るということになります。 つまり1.とは逆に 三角錐(A・DEF)=三角柱(ABC・DEF)/3 1 ∴ (三角錐の体積) = ―― (三角柱の体積)底面 と高さ が等しい二つの三角錐は、 分割合同ではない ので、その体積が等しいことは、なんらかの無限小分割の考え方を導入しないと、理解できないんですよ。 前振り2 でも、円の面積を求めるのに、円を細かい扇型に分割して各扇型の面積が 扇 型 の 弧 の 長 さ 半 径 であることから下図の三角錐の体積を算定しましょう。底面は三角形なので三角形の面積=底辺×高さ÷2です。あとは高さを掛けて3で割ればよいのです。 三角錐の体積=(底辺×高さ÷2)×三角錐の高さ÷3=(5×2÷2)×6÷3=10 三角錐の体積の公式は下記が参考になります。 三角錐の体積の公式は?



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



3
正四面体 三角錐の比 国立B https//youtube/g9xTqw8oZNo三角錐の切断の体積比公式! では、軽く証明のようなものをしていきましょう。図のように、三角錐を横に倒してみると、 まず、 \\frac{\triangle O E F}{\triangle O B C}=\frac{OE\times O F}{OB\times O C}\ (勝手に使ってますが、これを証明するのは難しくないので省略三角錐 一筆 書き 4 Appを購入またはダウンロードするにはMac App Storeを開いてください。, マッチ3タイプのパズルゲームです。 同じ色(同じ形)のタイルをタッチでなぞって一筆書きで3つ以上のタイルを白いラインで揃えてください。 一度にたくさんの




圆锥体的体积公式是怎么推导出来的 知乎




簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
2:三角錐ADEFと残る1つの三角錐(ウ)について。これらの三角錐の 底面はともに長方形(エ)を2等分したものと考えられます。その面積は 等しく、また 高さも同じですから、体積も等しくなります。したがって『三角錐ADEFと三角錐(ウ)の体積は等しい三角錐の体積 当HPの読者のK.S.さんより、平成24年10月10日付けで標記話題をメールで頂いた。 原点をOとし、空間上の3点A(a1,a2,a3)、B(b1,b2,b3)、C(c1,c2,c3)とする。 このとき、三角錐 OABC の体積Vは、次式で与えられる。 (証明1) 3点A(a1,a2,a3)、B(b1,b2,b3)、C(c1,c2,c3)を通る平面の方程式を ax+by+cz=1 とすると、原点Oかまったりのんびり図形など描いてみました。 3分の1 こんな簡単な数で 柱体と錐体 けりがつく そこに至るまでの 複雑な道を 見た目だけでも 簡単にしようと・・・ 見かけ倒しの徒労 三角錐=(三角柱の3分の1) を視覚的に示す 問題: 底面と高さが等しい2つの三角錐は体積も等しい(頂点がずれ



数学




7 棱柱 棱锥 棱台和圆柱 圆锥 圆台的体积 球的表面积与体积 每日头条
正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱 よって,1つの 三角錐 の体積は次式で表される. 三角錐 の体積= 1 2r2 × r × 1 3 →「底面積×高さ× 1 3 」になっている.三角錐の体積 三角錐の体積=底面積×高さ× 1 3 証明 三角柱を3つの三角錐に分解することで証明する. (Ⅰ)三角錐 eafc と三角錐 eafd について 三角柱 abcdef の側面 acfd は平行四辺形である. よって



Q Tbn And9gcsb4mynrcfbnw7ssvan 2akghlpvpeefed Mecaix Mlsw7tqba Usqp Cau




正立方體與正三角錐 1 Youtube
三角錐ABCD と 三角錐BDEF 角柱の体積が角 錐 ( すい ) の体積の 3分の1 になる理由を書いておきます。 ここで、 次の2点は既知とします。 底面積と高さが同じ角錐は同じ体積になる。 (これもいつか証明を書きます。 上に書いた錐の体積の公式とよく似た形の公式があることに気がつくでしょうか? ずばり,三角形の面積の公式です. (三角形の面積) = (底辺)× (高さ)× 1 2 ( 三角形の面積) = ( 底辺) × ( 高さ) × 1 2 なんとなく見た目が似ています.この2つの公式が似ている 簡単公式三角錐の体積の求め方がわかる3ステップ 三角錐の体積の求め方の公式は?? こんにちは!この記事をかいているKenだよ。タルト最高。 三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になる



1



正四面体和三角锥图片 万图壁纸网
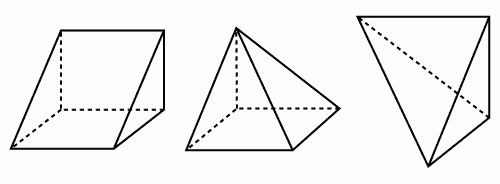
三角錐を一つ切り取る。さらに上下反対向きの三角錐をもう一つ切り取る。 すると残った少し妙な形の立体の体積はちょうど三角錐の体積と一致する。 したがって三角錐の体積は三角柱の体積の1/3 になる。」という記述があっ た。




求圆台体积公式的证明 附图




高中數學 空間幾何體的表面積和體積公式匯總及例題講解 人人焦點




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



知识点选 题智能组题平台



1




三角錐 四面体 の体積の公式 Schoolmath S Diary



简单的方法证明圆锥的体积 知乎



台体体积公式推导 哔哩哔哩 Bilibili



数学长征 不用积分推导 圆锥的体积公式 推导过程 圆锥 体积公式 推导



角錐の体積の公式は 1分でわかる公式 柱体の体積との違い 3分の1になる証明




錐體體積公式證明



坐标求四面体体积 正十二面体体积推导 一 Weixin 的博客 程序员宅基地 程序员宅基地




棱锥 Wikiwand




立体几何中与锥体体积有关问题的求解策略 雪花新闻




棱锥 Wikiwand



圆锥体积公式 万图壁纸网



四面体体积公式 知乎



为什么三棱锥体积是三棱柱的三分之一 数学



圆锥三分之一的理由 这时圆锥的体积是圆柱的三分之一 说明理由对还是错 朵拉利品网



球的体积公式简史兼打假阿基米德羊皮书 年6月30日未名空间存档 看帖神器



棱台体积公式证明图解 搜狗图片搜索




高中数学智库讲义 立体几何专题适用文科和理科初步 三一刀客
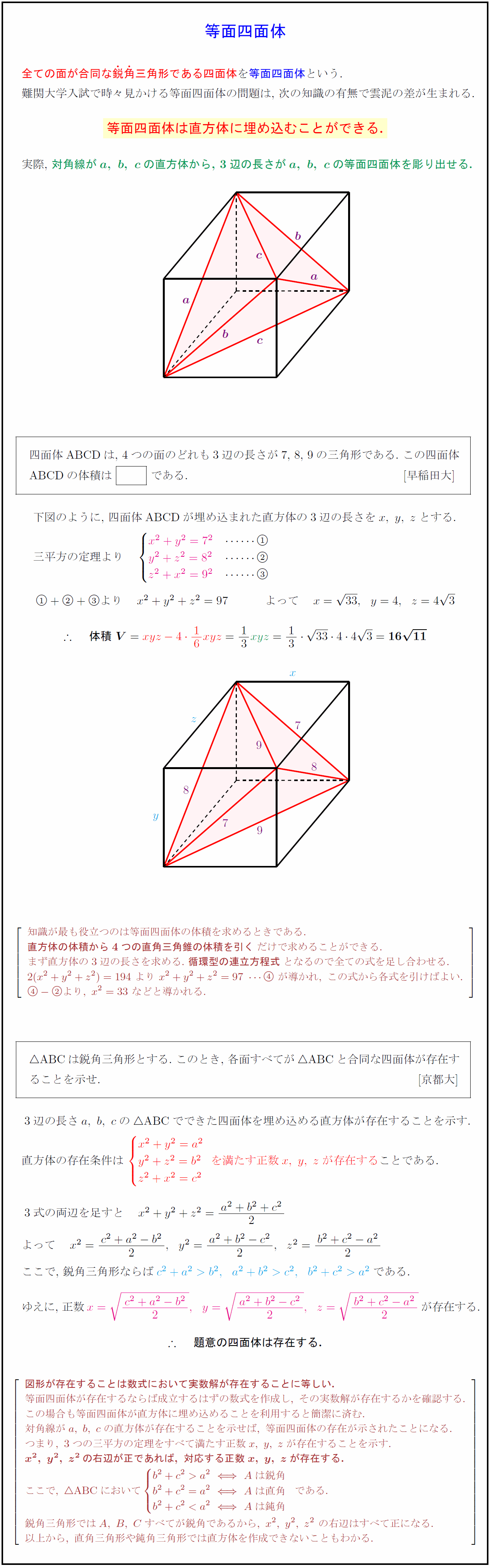



高校数学 等面四面体の体積と直方体への埋め込みと存在証明 受験の月




中国古代数学 第四章面积与体积第三节多面体体积 郭书春 在线阅读 九九藏书网



正四面体和三角锥图片 万图壁纸网



正三棱锥 快懂百科



求助 悲惨的小升初体积问题大学生都不一定会 教育资讯 早游戏




棱锥 维基百科 自由的百科全书



三菱锥形怎么画 万图壁纸网



悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube




三角錐體積
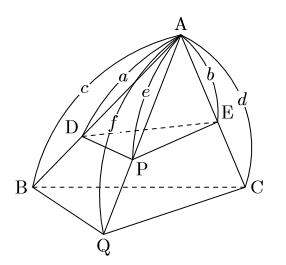



中学数学 公式 三角錐の体積比 数樂管理人のブログ




圆台 圆锥台体积 表面积 质量在线计算器 三贝计算网 23bei Com



棱台体积公式证明图解 搜狗图片搜索




等底等高的圆柱体是圆锥体的几倍 三人行教育网 Www 3rxing Org



两分钟搞清楚为什么椎体体积是柱体的三分之一 哔哩哔哩 つロ干杯 Bilibili



六棱柱体积公式 万图壁纸网



验证圆锥体积等于圆柱体积的三分之一 哔哩哔哩 Bilibili




三角立方体积计算公式 三角形体的立方怎么算 三角柱体积计算公式




直角四面体面积公式推导 北冥 的博客 程序员宅基地 直角四面体体积公式 程序员宅基地




三角錐 体積 ベクトル




四面体 Wikiwand
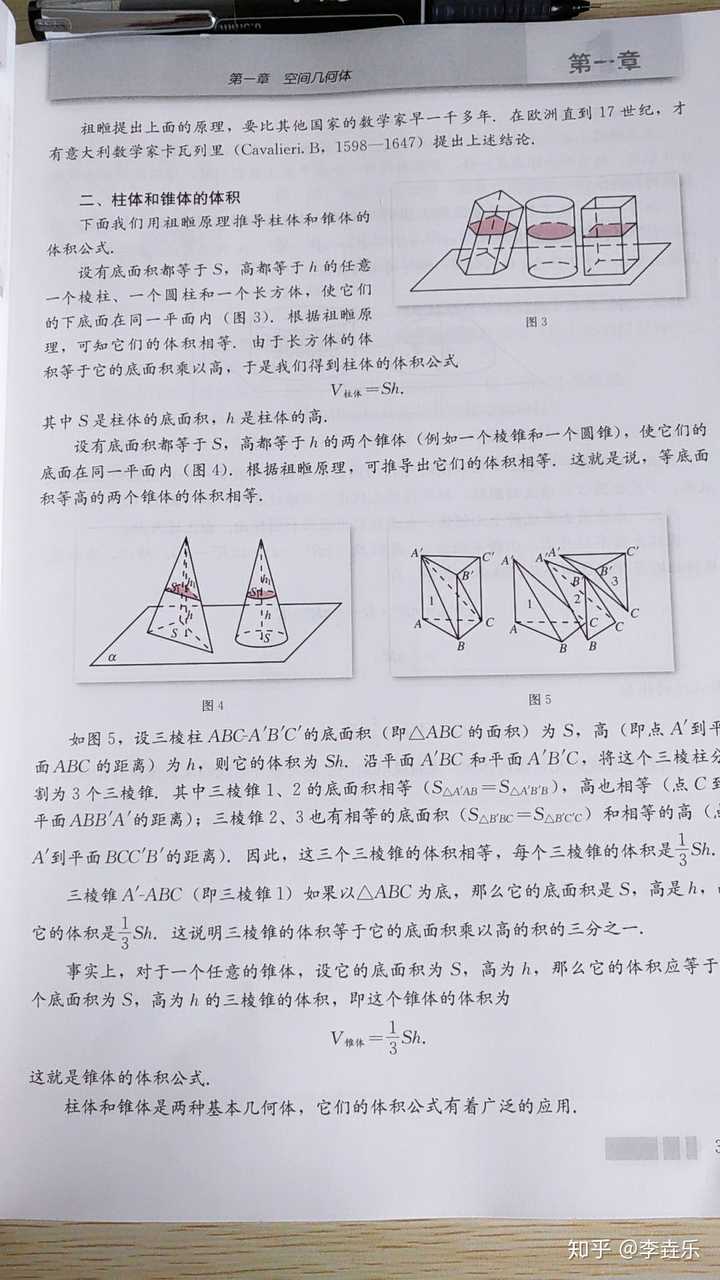



圆锥体的体积公式是怎么推导出来的 知乎




錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特



2



三角柱体积公式三角柱体积公式




23 6 圆锥的体积小學數學六年級 Youtube




錐體體積公式證明



数学一分钟球的体积公式推导证明 哔哩哔哩 つロ干杯 Bilibili




三角錐 体積比 証明



写真の公式の証明方法をお願いします Oa Aob B Of Yahoo 知恵袋




高中数学智库讲义 立体几何专题适用文科和理科初步 三一刀客




空間図形14 円すい台の体積 Youtube




祖氏原理与font Color Red锥体font体积公式费下载下载 Word模板 爱问共享资料




体积的公式怎么算的
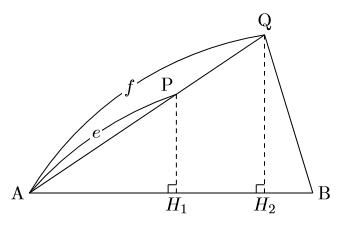



中学数学 公式 三角錐の体積比 数樂管理人のブログ



圆锥三分之一的理由为什么圆锥是圆柱的三分之一 朵拉利品网




錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特



圆锥三分之一的理由为什么圆锥是圆柱的三分之一 朵拉利品网
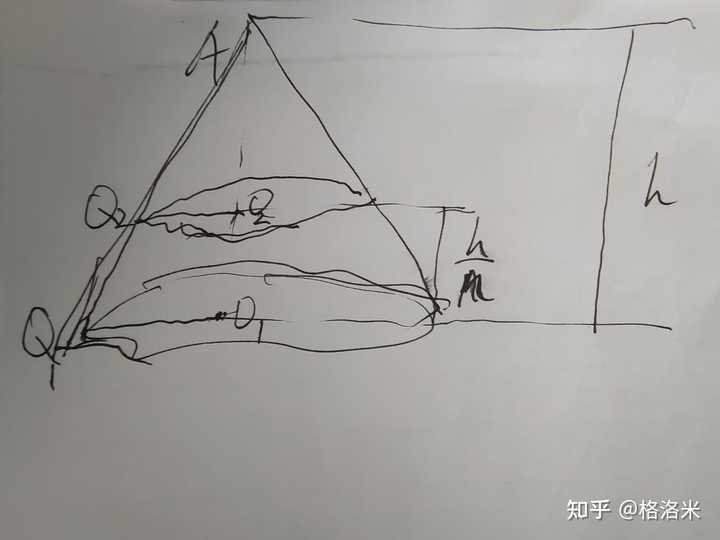



锥体的体积公式中1 3是怎么来的 知乎




圆锥体的体积公式是怎么推导出来的 知乎
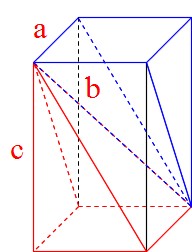



Mathematics 角錐の体積が角柱の3分の1になる証明 働きアリ




棱锥 Wikiwand




球的体积公式证明过程
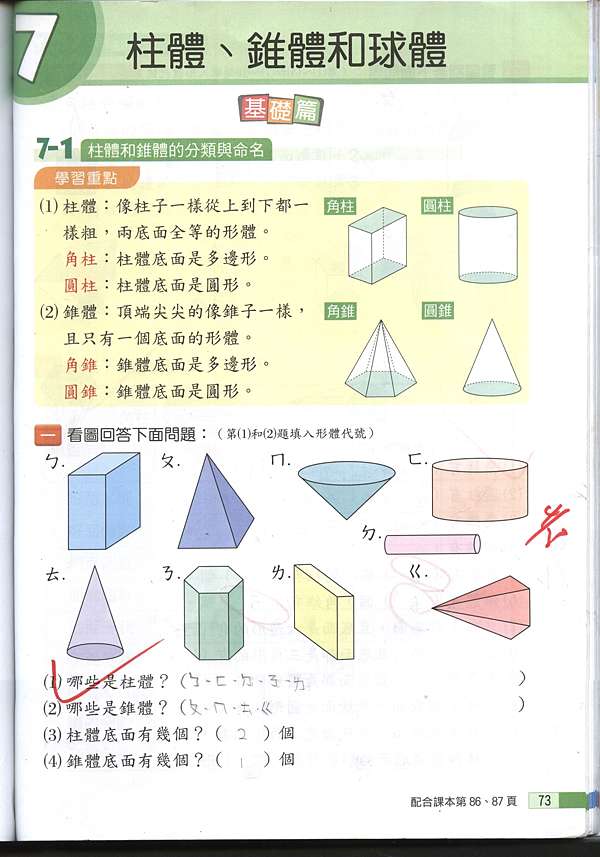



錐體體積公式證明



Hd限定三角柱体積公式 子供のための最高のぬりえ




四面體 维基百科 自由的百科全书




ベストオブ三角錐体積証明



棱台体积公式证明图解 搜狗图片搜索




立体几何中与锥体体积有关问题的求解策略 雪花新闻




球的体积公式证明过程




錐體體積 1 3柱體體積的3種證明法 Ishewh的創作 巴哈姆特




棱锥 Wikiwand




7 棱柱 棱锥 棱台和圆柱 圆锥 圆台的体积 球的表面积与体积 每日头条




三角錐体積公式 三角錐体積公式




三角錐 体積比 証明



简单的数学 初中生也能推导球的体积公式 叫我笑笑 哔哩哔哩 Bilibili
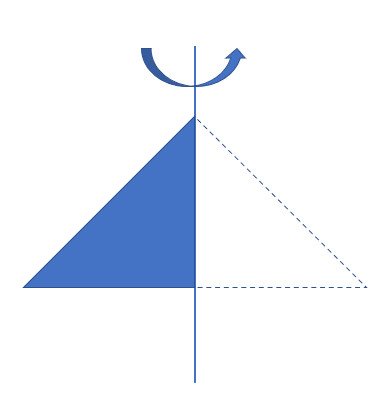



旋转体体积公式 Chenisok 博客园



锥体 信息阅读欣赏 信息村 K0w0m Com




不学好文言文 怎么拿下高考数学 新闻频道 手机搜狐



圆锥体的体积公式是怎么推导出来的 知乎



求体积 锥体及高维锥体体积公式推导 哔哩哔哩 つロ干杯 Bilibili




錐體體積公式證明




錐體體積公式證明




錐體體積公式證明
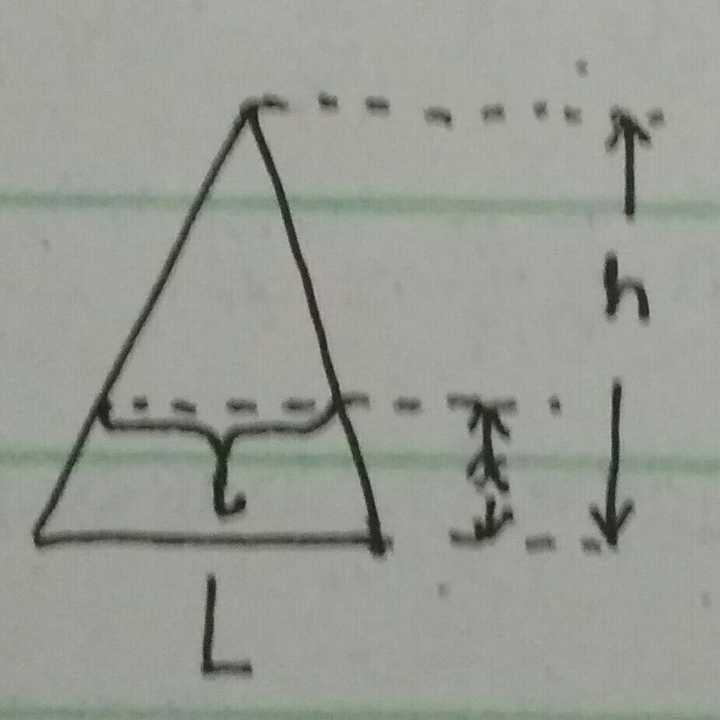



三角锥体体积 三角锥形的体积公式 三角体的体积公式




空間図形08 三角すいの体積比 Youtube




角錐體積公式的由來 Youtube
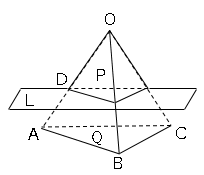



三角錐 体積比 証明



古人如何计算面积与体积 中国文化研究院 灿烂的中国文明



三角体的体积公式 搜狗图片搜索




高三立体几何证明题训练下载 Word模板 爱问共享资料



0 件のコメント:
コメントを投稿