++ 50 ++ y=x2乗分の1 162433-Y=x2乗分の1

 1/2乗がルートと等しくなる理由 さてそれでは、本題の解説に入りましょう。 今はまだ がどういうものか分かっていません。 しかし、 が であることは分かるはずです。 なぜならばすでに、 「 の 乗の 乗とは、 の 乗に等しくなる」 という事が定め定積分の計算には，そのうちどれか1つの原始関数を用いればよいが，計算が簡単なように C=0 となるものを用いる． すなわち， n F (x) C = (F (b) C )− (F (a) C )=F (b)−F (a) となり，どんな C の値を用いても差で消えるので，計算が最も簡単になる C= 0 の場合をなぜ2分の1乗がルートなのか 例えば、$(5^2)^3=5^6$ というように、$5$ という数を $2$ 乗 してから $3$ 乗 したものは、 $2\times 3=6$ 乗 したものと同じです。 これと似たような法則 「 $\dfrac{1}{2}$ 乗 してから $2$ 乗 したものは、 $1$ 乗 したもの」

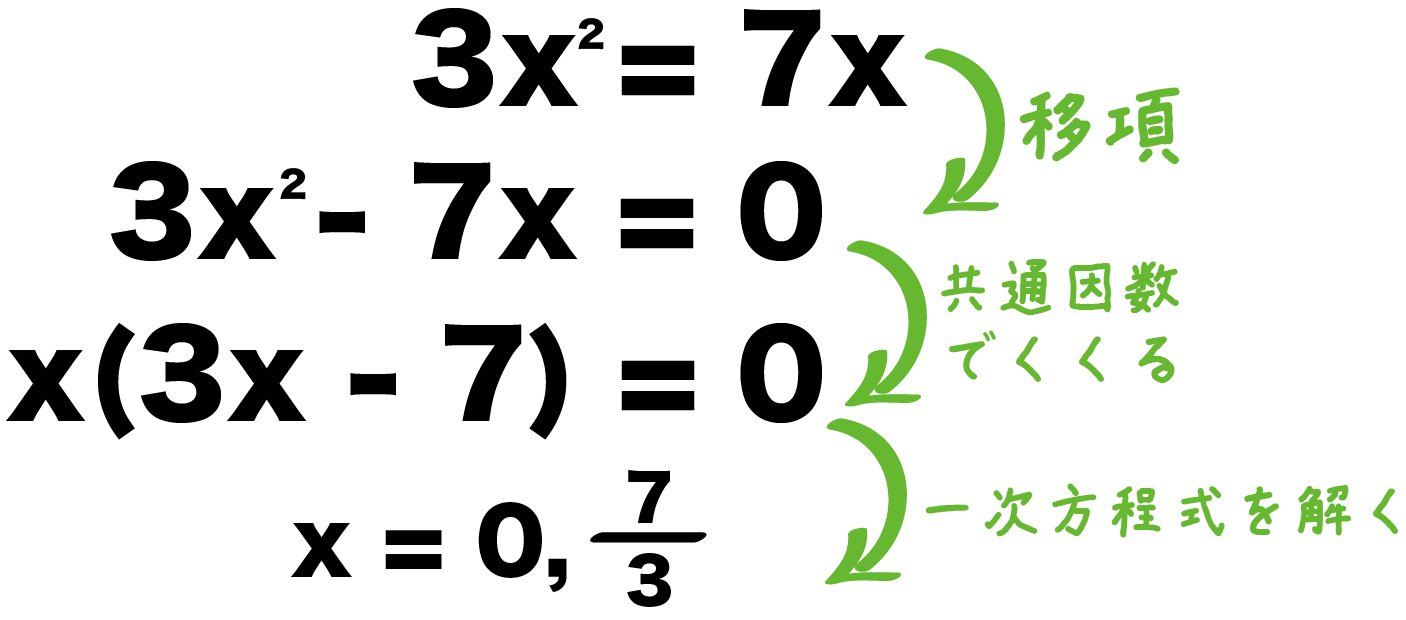
中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく

Y=x2乗分の1

Y=x2乗分の1-合成関数の微分公式と例題7問 レベル ★ 基礎 極限，微分 更新日時 合成関数の微分は（かたまりで微分）×（かたまりの微分） 合成関数を微分する方法を2通り紹介します。 また，合成関数の微分について7つの例題を解説します。 目次 合成のグラフは, a>0 の場合、右図のようになります。 a>0の場合、xの正負にかかわらず、yは常に正の値をとっています。 また、y軸に対し左右対称であることも分かります。 そして座標平面において、1次関数が直線、反比例関数が双曲線を描くのに対し、

Y Xの2乗分のx2乗 1の式を微分してグラフを書く問題があります Yahoo 知恵袋

平方完成は以下の手順で行うとよい。 ① x を含む項だけ、 x2 の係数でくくる ② x の係数を半分にして、2乗を足し引きする ③ 因数分解する ④ 分配法則を用いる ⑤ 定数項を計算する 例えば、3 x2 12 x 6を平方完成すると、 となる。 について、右図のような2次関数になり， x=1 （このとき y=1 ）のとき最大値 1 になる． 例題12 x2y=3 のとき， 2x 2 y 2 の最小値を求めてください． 条件式の方程式を使って1文字を消去しますが， y を消去すると初めから分数が登場します． この形なら x を消去 よって、 ∫x^ (a1)dx＝ (1/a)*x^a＋C →∫x^adx＝ {1/ (a1)}*x^ (a1)＋C となります。 つまり、 ∫1/x^2 dx＝∫x^ (2)dx ＝ {1/ (21)}*x^ (21)＋C ＝－x^ (1)＋C ＝－1／x＋C

つまり， を2乗すると3になりますね。 では， を2乗してみると，どうなるでしょうか？ ここで，①，②より， と言えます。 この両辺の（ ）の中を比較して， となります。 一般に， と定義します。 例えば， ， です。 さらに，指数が， ではなく， の場合はどうなるかを考えましょう。 は，本当は， の2を省略して書いたものなのです。 つまり，3の 乗が とグラフの縮小率： （0～1推奨） 指数関数のグラフ y=() 数式直接入力 y= x 25は、{x^2}5と書きます。 例：y={(1/2)^x}1（2分の1のx乗プラス1） 使い方 式の入力には、数字と「x * / ( ) { }」を使用します。すべて半角です。 ×は「*」、÷は「/」を用います。「yはxの2乗に比例」⇒y＝ax 2 中学1年生のときに学習した「比例」という言葉を覚えているかな？ yとxについて 「yはxに比例する」 という関係があるとき、その式は y＝ax（aは比例定数） と表せた

Xのn乗の微分公式 (xn) ′ = nxn − 1 ( n は 実数 ) 最も基本となる公式 (1 x) ′ = − 1 x2 (√x) ′ = 1 2√x (xn) ′ = nxn − 1 に n = − 1 や n = 1 2 を代入すると求まる熊本大学数理科学総合教育センター x12 重積分の変数変換 演習問題1 解答 ˇ 問題の難易度の目安基礎9 標準8 発展8 1(9)(変数変換1) 次の各問いに答えよ． (1)変数変換x = u2;より，解は (2x3)(x1) となります。このように,1･3,2･1と表のの中の数値を対角線上に掛けることから，このような因数分解を｢たすきがけ｣の因数分解と呼ばれています。 練習問題2 次の式を因数

Y Xの2乗分のx2乗 1の式を微分してグラフを書く問題があります Yahoo 知恵袋

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

左辺にxの式の2乗 を作るために両辺に数字をたす。 (例3)の場合はxの係数が6 → x 2 6x が9なら、(x3) 2 と因数分解できるので両辺に9をたす。 x 2 2axa 2 = (xa) 2 の因数分解は xの係数が2 a なので (x a) 2 が作れる。 (例4) x 2 8x = 1X2乗=9 x2乗=5 計算結果を下記に示します。 となります。2次方程式の計算方法は下記をご覧ください。 2次方程式とは？1分でわかる意味、解き方、解の公式、因数分解との関係 x（エックス）の2乗と2xの違い xの2乗と2xは意味が全く違います。解説 関数 y = f(x) の x = a における微分係数は次の式で定義されます。 f'(a) = または f'(a) = 微分係数は，個々の定数 x = a の値に対して定まりますが， x の値にその微分係数を対応させる関数と見たとき， f'(x) = または f'(x) = を，関数 y = f(x) の導関数（または微分）といいます。

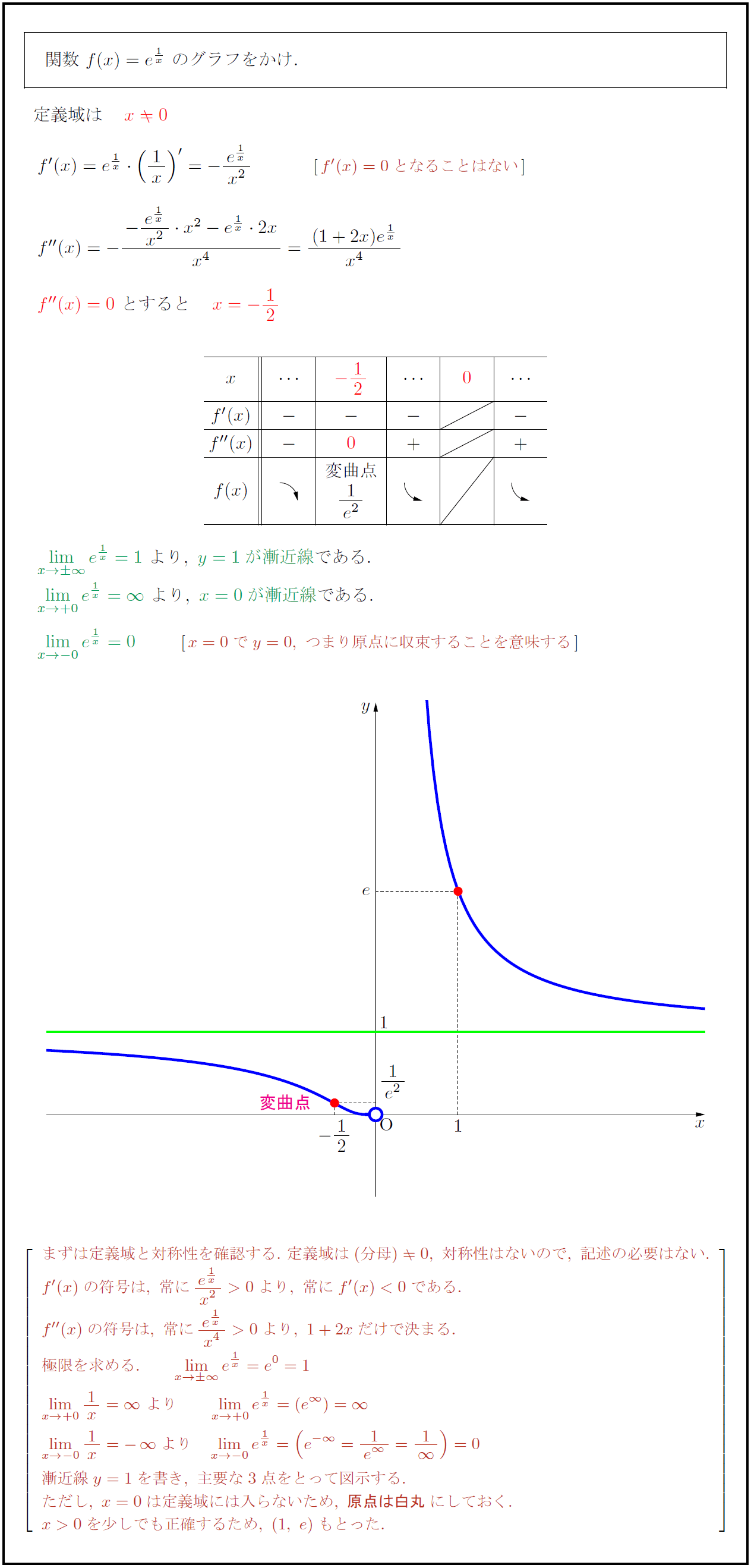
高校数学 指数関数 Y E 1 X のグラフ 受験の月

Eの2x乗の微分や積分は Eの3x乗の微分や積分は Eのマイナスx乗の微分や積分は E 2x E 3x E X ウルトラフリーダム

上でやったように左辺がxの式の2乗で右辺が数字であれば2次方程式を解くことが出来る。 この考え方をつかって(例3)を解く。 (例3) x 2 6x = 1 →左辺をxの式の2乗にするため両辺に9を足す。 x 2 6x9 = 19 →左辺を因数分解すると(x3) 2 になる。 (x3) 2 = 10 →ここからは(例2)でやったのと 3 x 2 − 7 x 2 のように「共通する因数でくくっても、 x 2 の係数が 1 にならない式」を因数分解する場合には、「たすきがけ」というテクニックを使います。 文字だけだとピンと来にくいと思うので、具体例を通じてやり方を見ていきましょう。 問③． 3 x (1)の問題で関数Y=x2乗1を平方完成をしないのは二次関数と書いてないからですか？ 数学 y=2(x1) ²を二次関数のグラフで頂点を求めると言う問題なのですが、1、0になるときの細かい式を教えて下さい！

Y X X2乗 1のグラフ 画像の答えが理解できません なぜ Yahoo 知恵袋

3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書

オープニング（1分55秒） 円 x 2 ＋y 2 ＋lx＋my＋n＝0（5分38秒）;通常，式の展開は次のような順序で，「総当たりで」掛けると考えることが多いが，二項定理，多項定理の解説はこの方法では分かりにくいので，「代表選手の選び方」で解説してみる． 右図のように各々の（ ）からどちらか1つの項 a , b を選んで なので、 (x^n)' = n x^ (n1) これが、べき乗の 微分 の公式だ。 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ いま、上で見てきたことの逆が「 積分 」だ。 微分 が 「すぐ隣同士の引き算」 なら、 積分 とは 「すぐ隣同士の足し算」 のことだ。 x^2 の 積分 が (1/3) x^3 になるとは、 正方形を重ね合わせて作った立体の体積が

1

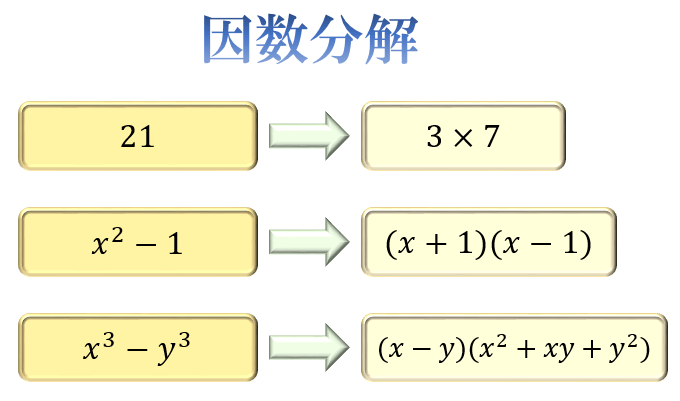
因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

 発展的な三角関数の積分公式 ここから先は公式を丸覚えするというよりも導出方法をしっかり理解することが大事です。 ∫ 1 sin ⁡ x d x = 1 2 log ⁡ ( 1 − cos ⁡ x 1 cos ⁡ x) C \displaystyle\int \dfrac {1} {\sin x}dx=\dfrac {1} {2}\log (\dfrac {1\cos x} {12乗に比例する関数 2乗に比例する関数の式 y=ax 2 (aは比例定数) yの値を求める。 関数はxの値に対応して、yの値が1つ定まるので、関数の式が分かっている場合、 xに値を代入することでyの値を求めることができる。 y=3x 2 で x=2 のときのyの値を求める。 式にxの値を代入すると 1 3分の1a2乗π(√31)a2乗の答えが(√3112分の1π)a2乗なのですが、どう計算した 2 因数分解がわかりません 4x2乗4xyy2乗2xy x2乗2xyy2乗xy 9x2乗 3 数学分数の読み方を教えてください。 2 4 1 3 だと読みは「3分の1分の4分の2

この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave

2 の問題を教えて下さい 何で最後にx2乗を引いてるんですか 2 高校 教えて Goo

§1 2次関数 2．2次関数のグラフ(1) 2次関数のグラフは，放物線とも呼ばれ，ボールを遠投したとき描く曲線のような形をしています。その曲線を式で書くと，y=ax 2 (a≠0) の形に書かれます。 この章では，この曲線について，前の章で学んだ平行移動を行なうことにします。で求めることができます． f (x, y) が連続関数で，各変数の定義域が a≦x≦b, α≦y≦β であるとき,この重積分は β∫ αwww b∫ awww f (x, y)dx dy (1) または b∫ awww β∫ αwww f (x, y)dy dx (2) のように，1変数の積分の繰り返しによって行うことができます もう少し簡単な式から考えてみましょう。 (x1)2乗 = x2乗2x1 はわかりますよね？ (xa)2乗 = x2乗2axa2乗 も大丈夫かな？ 下の式で、右辺のa2乗を左辺に移動しましょう。 どうなりますか？ これと今回の問題を比べて見てください。 こういう変形に慣れると、問題を解く力がワンランク上がります。 2 (a－1)xを展開してから平方完成していたので間違ってました

Y ｘ二乗 ｘの微分を教えてください Peing 質問箱

これがわかりません Clear

式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味，関数 y = ax2 y = a x 2 のグラフの特徴，直線の式の求め方を理解するA x の微分法 a x をxで微分するとどうなるか考えてみよう。 まずは、底の変換をして、微分することをやってみよう。 いいかな。結果は覚えておこう。 つぎに、両辺の対数をとる方法。 eのx乗を微分したら何になりますか？ 高校 締切済 教えて！goo

2次関数の問題で Y X２乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋

中3数学 Y 2分の1x2乗のグラフと変域 5分で学習 Youtube

サイン分の1，コサイン分の1の積分 レベル ★ 最難関大受験対策 積分 更新日時 ∫ 1 sin ⁡ x d x = 1 2 log ⁡ ( 1 − cos ⁡ x 1 cos ⁡ x) C \displaystyle\int \dfrac {1} {\sin x}dx=\dfrac {1} {2}\log\left (\dfrac {1\cos x} {1\cos x}\right)C ∫ sinx1 dx = 21

X 1分のx X2乗 2x 3分の3x 1の解き方を教えてください Yahoo 知恵袋

数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

Yx2乗 ニスヌーピー 壁紙

指数 対数関数 ２分の１乗の意味 数学 定期テスト対策サイト

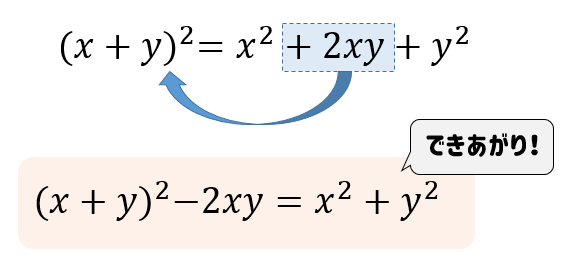
二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ

二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ

19 号 放射線治療計画における分画選択ツール Astamuse

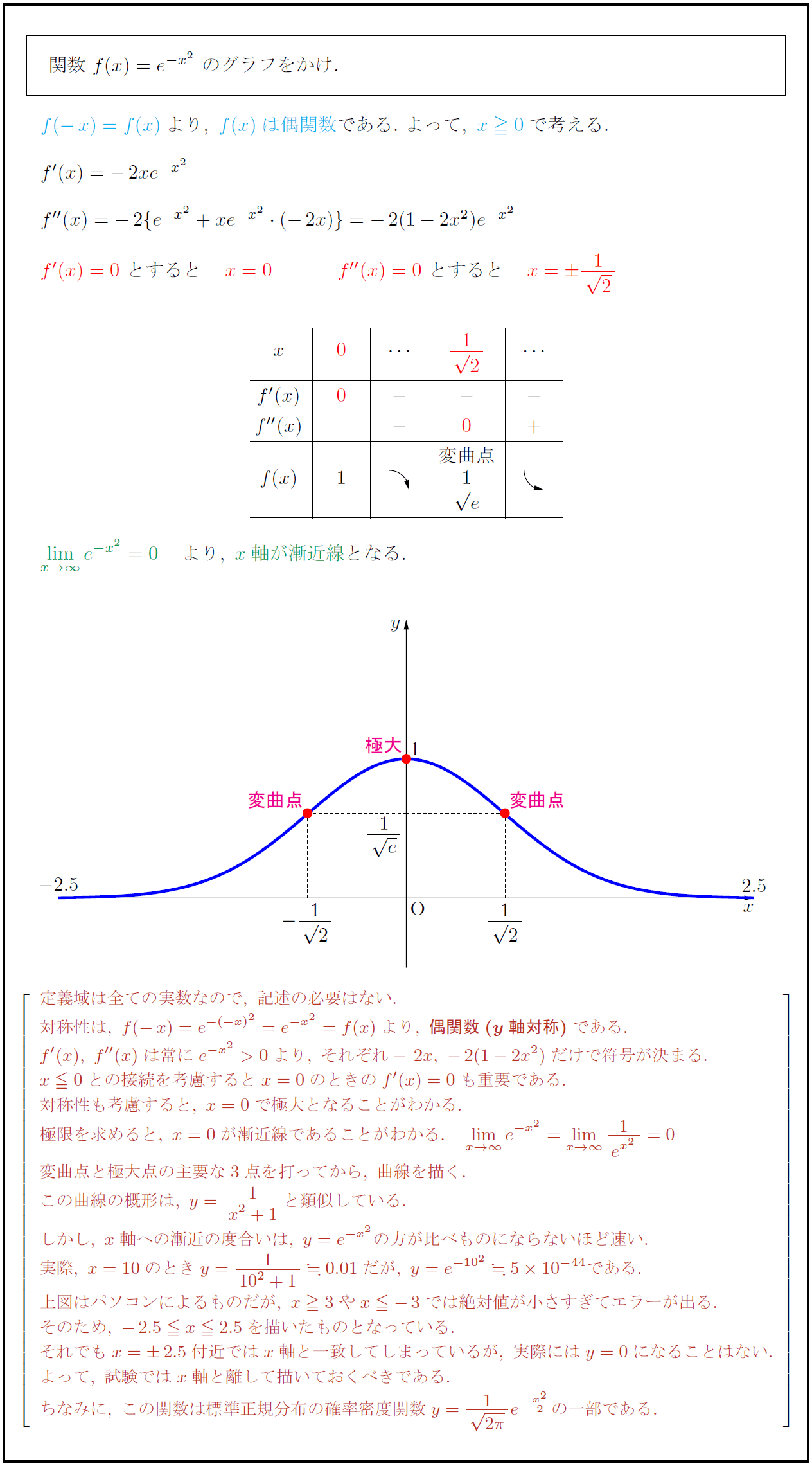
高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月

3分の２乗の説明

Xの二乗分の1 ｙの2乗分の一を通分するとなぜxの2乗ｙの2乗分のxの二乗 Yahoo 知恵袋

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い

3分の２乗の説明

Y 1 X2乗のグラフ Youtube

X 1分のx2乗 X分の1の解き方を教えてください ただの通分 Yahoo 知恵袋

中3数学 Yはxの2乗に比例 とは 映像授業のtry It トライイット

Y 1 X2乗のグラフ Youtube

Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋

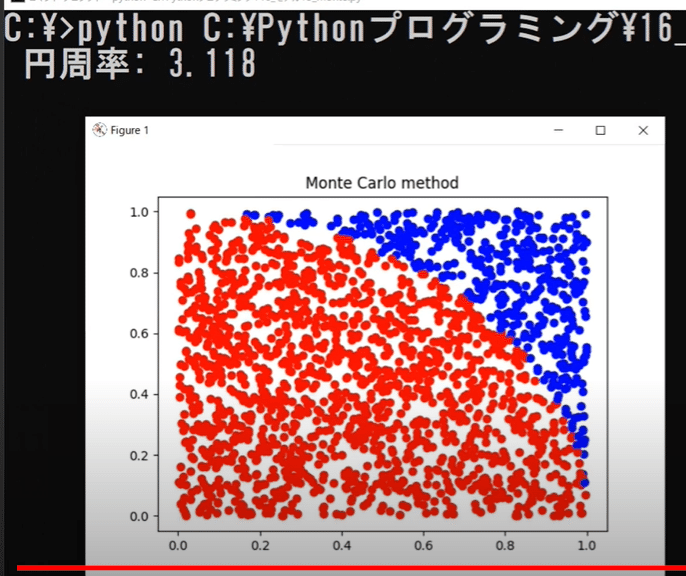
高校情報１ シミュレーション 確定モデル 確率モデル 円周率とモンテカルロ法 Pythonプログラミング 教員研修用教材 学習16 高校情報科 情報処理技術者試験対策の突破口ドットコム Note

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

3分の２乗の説明

2次関数のｙ ２分の１ｘ２乗の票の作り方を教えて下さい 2次 Yahoo 知恵袋

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

X 1分のx2乗 X分の1の解き方を教えてください ただの通分 Yahoo 知恵袋

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

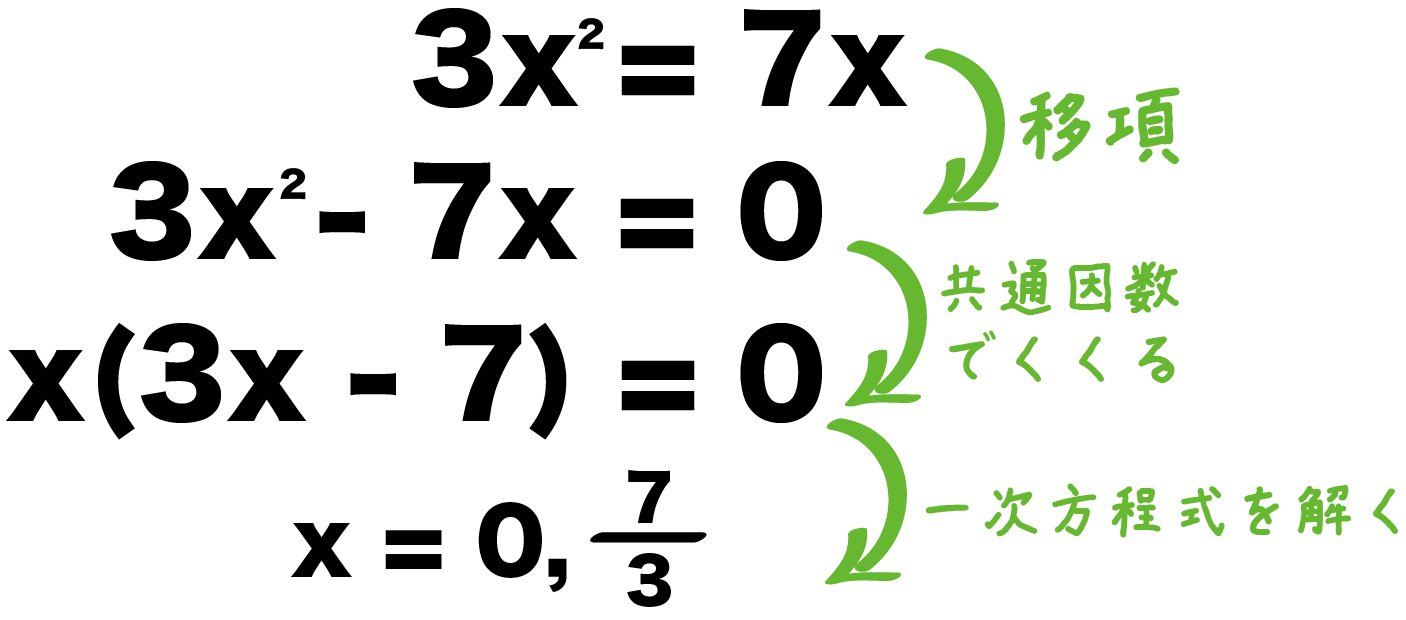
中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく

差分和分 怜悧玲瓏 高校数学を天空から俯瞰する

この2問の解き方を教えてください 答えは 5 が 6 が です Clear

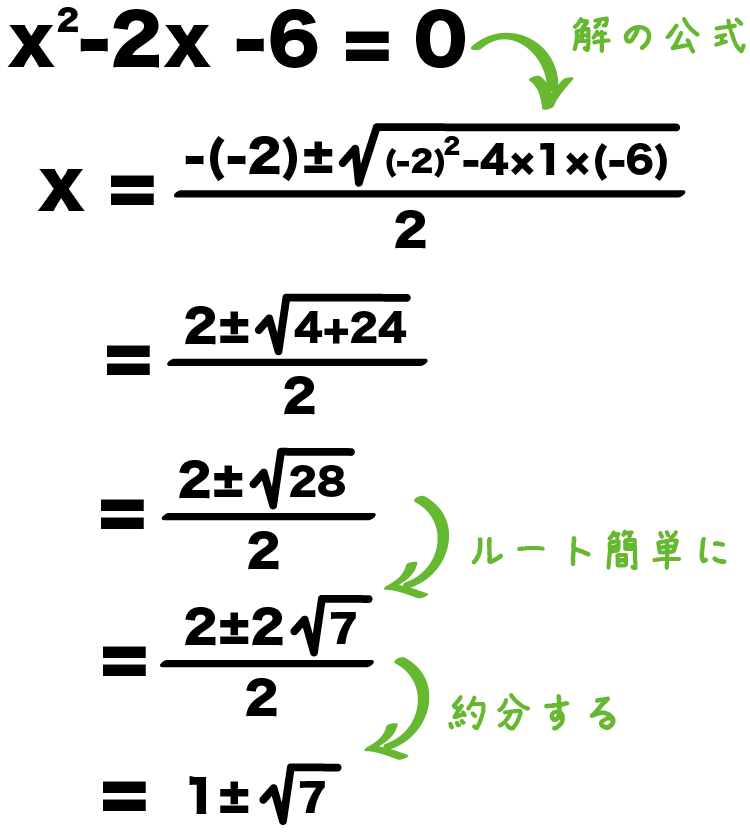
中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく

高校数学です 二次関数y X 6xのグラフを書け また その軸と頂点 高校 教えて Goo

2 裏業

Www Hiragaku Ac Jp Challenges Pdf 6 18 6 E6 9c 18 E6 97 A5 E9 85 8d E4 Bf A1 80 802 E5 B9 B4 E7 B9 E9 80 B2 E7 90 86 E7 80 80 E6 95 B0 E5 Ad A6 E2 85 A1 E5 9b E5 81 A8 E6 96 B9 E7 A8 8b E5 8f E2 91 A0 Pdf

Xの2乗 Xの2乗分の1 7の時t X X分の1とおくとtの2乗 Yahoo 知恵袋

Y 1 X ２乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo

Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋

数学です Y 1 X 2のグラフで X 2のときは X 2に近づくと無限大に発散す 数学 教えて Goo

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube

Y 3分の1ｘ2乗 2ｘのグラフの ｘ切片の求め方を教えて下さい Y 0のときの途中 Clear

Y ｘ二乗 ｘの微分を教えてください Peing 質問箱

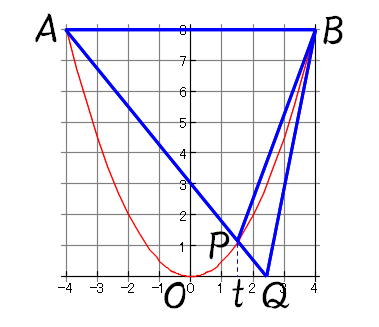
Mathematics ２乗に比例 放物線 応用問題の解き方 関数と図形 面積の二等分 等積変形 働きアリ

Mathematics 関数と証明 大阪府公立 ２２年前期理数科 働きアリ

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

1

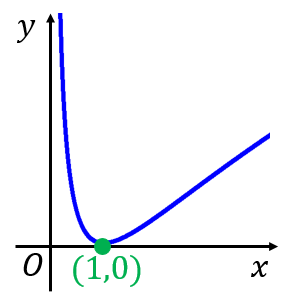
Y Logx 2の微分 積分 グラフ 具体例で学ぶ数学

偏微分の意味とやり方

中学数学 文字を用いた四則計算

Yx2乗 ニスヌーピー 壁紙

高校数学 因数分解 4乗が登場する式の因数分解 置き換えをして見慣れた形に直して解こう 数学の面白いこと 役に立つことをまとめたサイト

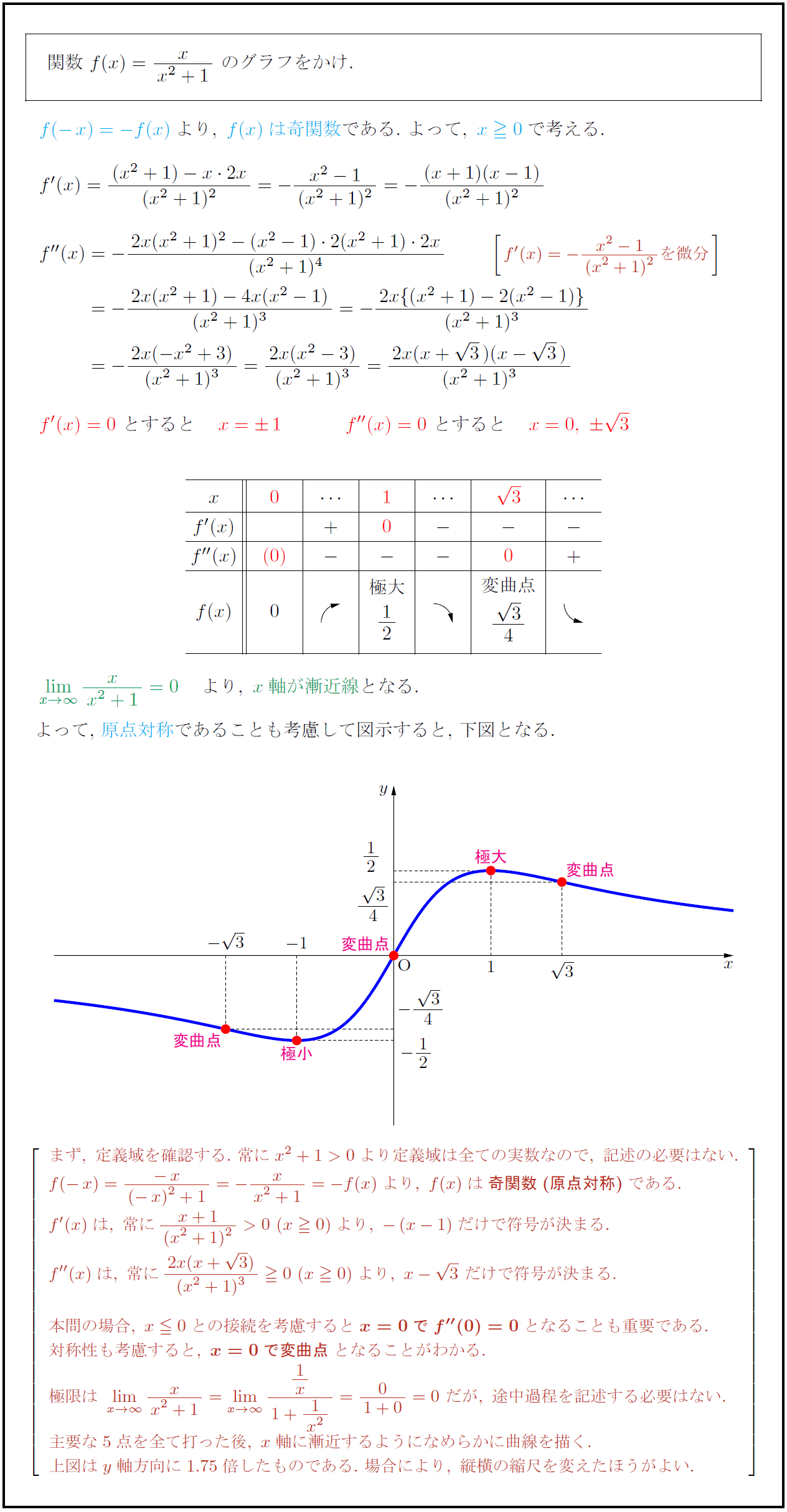
高校数学 分数関数 Y X X 1 のグラフ 受験の月

1

Eの2x乗の微分や積分は Eの3x乗の微分や積分は Eのマイナスx乗の微分や積分は E 2x E 3x E X ウルトラフリーダム

3

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

なぜ4のx乗分の1が2分の1のx乗の2乗になって Clear

因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

Xのマイナス２乗とxのマイナス2分の1乗は何になりますか Clear

二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い

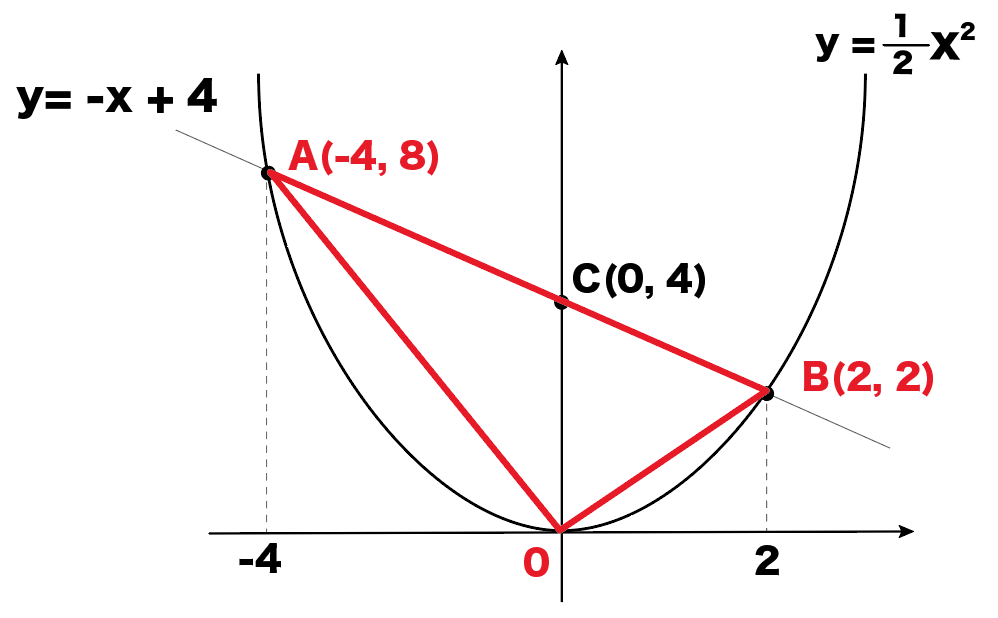
二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく

因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

Xの二乗分の1 ｙの2乗分の一を通分するとなぜxの2乗ｙの2乗分のxの二乗 Yahoo 知恵袋

Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf

高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト

数学小話 いろいろ拡張しよう マイナス2分の1乗とは 日比谷高校のススメ

数学 中3 35 二次関数のグラフ Youtube

高校数学 2次関数がx軸から切り取る線分の長さ 受験の月

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

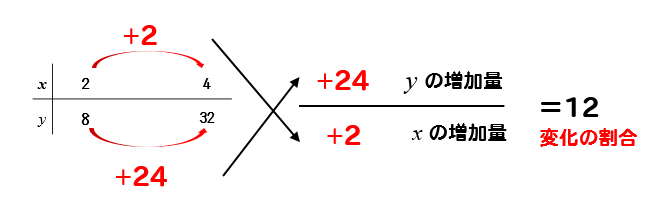
変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ

Y 2分の1xの二乗 の軸と頂点はどうなりますか また X 3 Yahoo 知恵袋

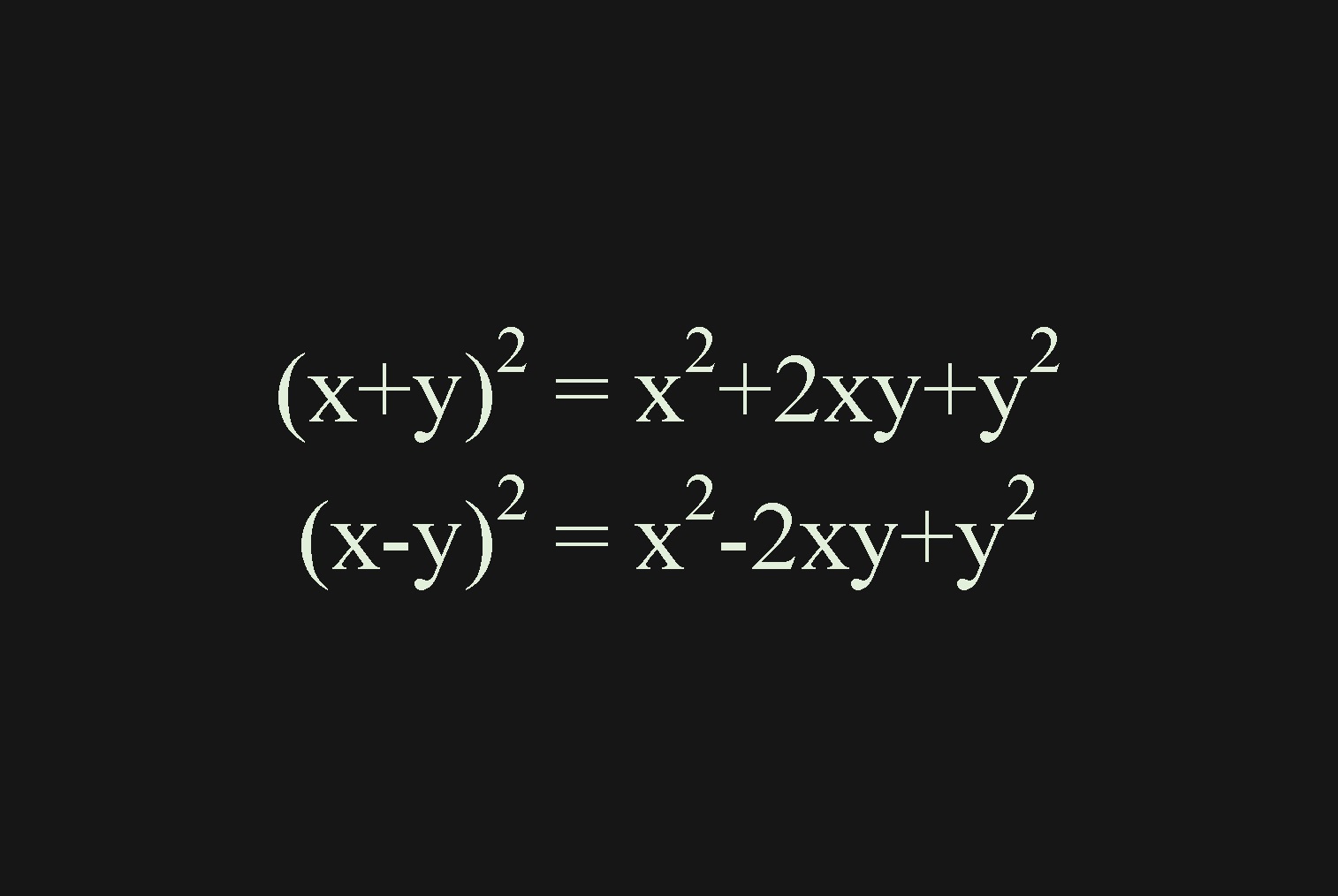
指数法則の一覧 統計学でよく使うもの 統計学が わかった

1 12公式 3次関数 おいしい数学

２次関数のグラフ

放物線y X 2 0 X 1 の長さ 身勝手な主張

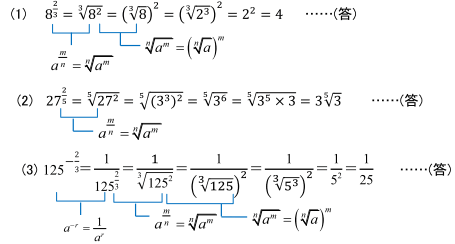
３ ２乗 マイナス２分の３乗 の計算の仕方 数学 苦手解決q A 進研ゼミ高校講座

Http Www Ikushin Co Jp Shuppan Textimg 16jack Chu3hyo Sugaku Hon Pdf

2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター

中3数学 Y X2乗のグラフ 5分で学習 Youtube

中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube

点pが放物線y X2乗 1上を動くとき 定点a 2 1 と点pを結ぶ線分の中点の軌 Clear

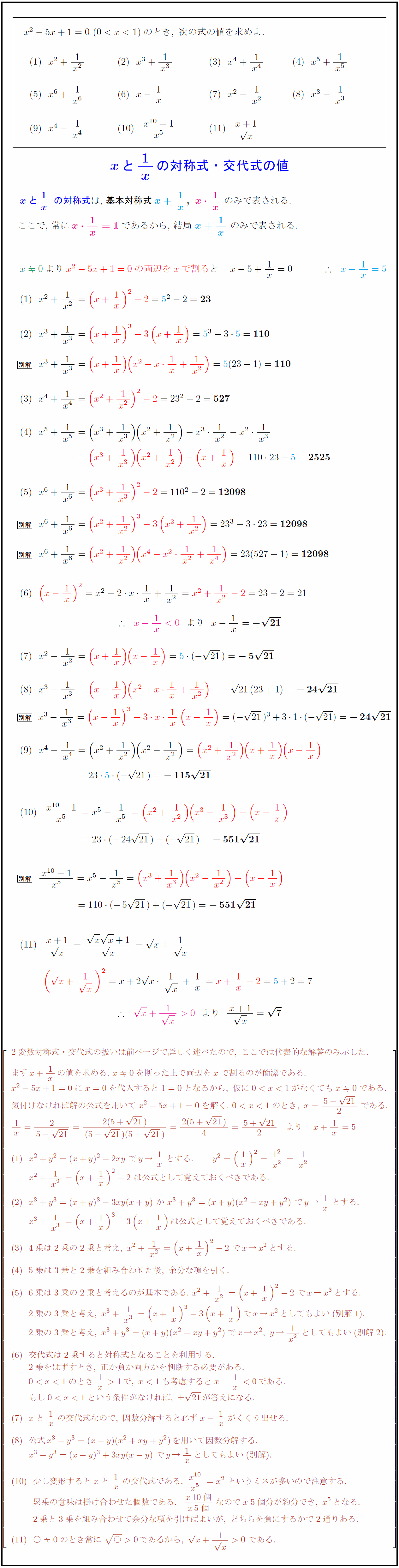
高校数学 Xと1 Xの対称式 交代式の値 X 1 X X 1 X X 1 X など 受験の月

Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

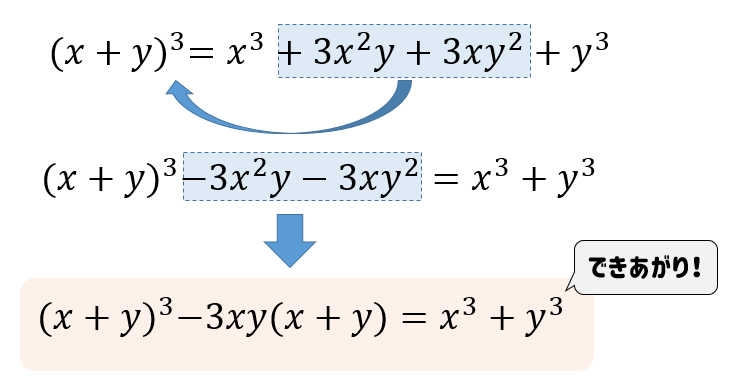
二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ

Yx2乗 ニスヌーピー 壁紙

2 裏業

Yx2乗 ニスヌーピー 壁紙

高校数学です 二次関数y X 6xのグラフを書け また その軸と頂点 高校 教えて Goo

因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

Incoming Term: y=x2乗分の1,